题目内容
14.课堂上老师指出:若a,b,c是△ABC的三边长,且满足a2+b2+c2-ab-bc-ac=0,请判断该三角形的形状.小明在与同学一起合作探究这个问题时,说出了自己的猜想及理由,得到了老师的赞扬.请你写出小明的猜想和理由.分析 由a、b、c是△ABC的三边可知,三边都大于0,解其方程得到a=b,b=c,c=a,从而知道三角形一定是等边三角形.
解答 解:依题意得:$\frac{1}{2}[{{{({a-b})}^2}+{{(b-c)}^2}+{{(c-a)}^2}}]=0$
所以(a-b)2+(b-c)2+(c-a)2=0
所以a=b,b=c,c=a.
故△ABC是等边三角形.
点评 本题考查了因式分解的应用,利用三角形三边都大于0这一条件,解其方程而判定为等边三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在直角坐标系中,点P(2,3)到原点的距离是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{13}$ | C. | $\sqrt{11}$ | D. | 2 |
19.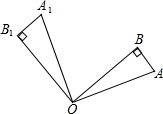 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
 如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )
如图,Rt△OAB中,∠AOB=25°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB为( )| A. | 125° | B. | 65° | C. | 75° | D. | 50° |