题目内容
 如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.
如图,已知线段AB∥CD,AD与BC相交于点K,E是线段AD上一动点.(1)若BK=
| 5 |
| 2 |
| CD |
| AB |
(2)连接BE,若BE平分∠ABC,则当AE=
| 1 |
| 2 |
分析:(1)由已知得
=
,由CD∥AB可证△KCD∽△KBA,利用
=
求值;
(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG=
BC,而GF=
CD,EF=
AB,利用EF=EG+GF求线段AB、BC、CD三者之间的数量关系.
| CK |
| BK |
| 2 |
| 5 |
| CD |
| AB |
| CK |
| BK |
(2)AB=BC+CD.作△ABD的中位线,由中位线定理得EF∥AB∥CD,可知G为BC的中点,由平行线及角平分线性质,得∠GEB=∠EBA=∠GBE,则EG=BG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)∵BK=
解:(1)∵BK=
KC,
∴
=
,
又∵CD∥AB,
∴△KCD∽△KBA,
∴
=
=
;
(2)当BE平分∠ABC,AE=
AD时,AB=BC+CD.
证明:取BD的中点为F,连接EF交BC于G点,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG=
BC,而GF=
CD,EF=
AB,
∵EF=EG+GF,
即:
AB=
BC+
CD;
∴AB=BC+CD.
 解:(1)∵BK=
解:(1)∵BK=| 5 |
| 2 |
∴
| CK |
| BK |
| 2 |
| 5 |
又∵CD∥AB,
∴△KCD∽△KBA,
∴
| CD |
| AB |
| CK |
| BK |
| 2 |
| 5 |
(2)当BE平分∠ABC,AE=
| 1 |
| 2 |
证明:取BD的中点为F,连接EF交BC于G点,
由中位线定理,得EF∥AB∥CD,
∴G为BC的中点,∠GEB=∠EBA,
又∵∠EBA=∠GBE,
∴∠GEB=∠GBE,
∴EG=BG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵EF=EG+GF,
即:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=BC+CD.
点评:本题考查了平行线的性质,三角形中位线定理,相似三角形的判定与性质,角平分线的性质.关键是构造平行线,由特殊到一般探索规律.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


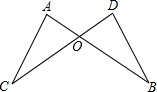 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.