题目内容
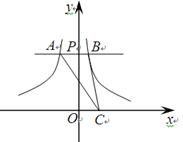
 如图,点A在x轴正半轴上OB=4,∠AOB=30°,BA⊥x轴于A.
如图,点A在x轴正半轴上OB=4,∠AOB=30°,BA⊥x轴于A.
(1)画出△AOB绕点O逆时针旋转后90°后的图形;
(2)直接写出旋转变换后点B的对应点B′的坐标;
(3)求旋转过程中线段OA、OB所扫过的重叠部分的面积.
解:(1)△AOB绕点O逆时针旋转90°后的△A′OB′如图所示;
(2)∵OA=4,∠AOB=30°,
∴AB=OA•tan30°=4× =
= ,
,
∴点B′(- ,4);
,4);
(3)∵∠AOB=30°,
∴∠A′OB=90°-30°=60°,
∴线段OA、OB所扫过的重叠部分的面积= =
= π.
π.
分析:(1)在y轴正半轴上截取OA′=OA,过点A′作A′B′⊥y轴,截取A′B′=AB,连接OB′,即为旋转后的三角形;
(2)解直角三角形求出AB,再根据点B′在第二象限写出坐标即可;
(3)求出∠A′OB,再根据图形,重叠部分为以OA′为半径以∠A′OB为圆心角的扇形,然后利用扇形的面积公式列式计算即可得解.
点评:本题考查了利用旋转变换作图,扇形的面积公式,坐标与图形变化-旋转,熟记旋转的性质确定出点A′、B′的位置是解题的关键.

(2)∵OA=4,∠AOB=30°,
∴AB=OA•tan30°=4×
 =
= ,
,∴点B′(-
 ,4);
,4);(3)∵∠AOB=30°,
∴∠A′OB=90°-30°=60°,
∴线段OA、OB所扫过的重叠部分的面积=
 =
= π.
π.分析:(1)在y轴正半轴上截取OA′=OA,过点A′作A′B′⊥y轴,截取A′B′=AB,连接OB′,即为旋转后的三角形;
(2)解直角三角形求出AB,再根据点B′在第二象限写出坐标即可;
(3)求出∠A′OB,再根据图形,重叠部分为以OA′为半径以∠A′OB为圆心角的扇形,然后利用扇形的面积公式列式计算即可得解.
点评:本题考查了利用旋转变换作图,扇形的面积公式,坐标与图形变化-旋转,熟记旋转的性质确定出点A′、B′的位置是解题的关键.

练习册系列答案
相关题目
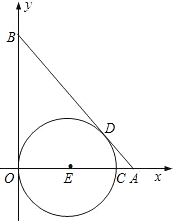 相切于点D,已知点A的坐标为(3,0),点B的坐标为(0,4).
相切于点D,已知点A的坐标为(3,0),点B的坐标为(0,4). (2013•海门市二模)如图,点P在y轴正半轴上运动,点C在x轴上运动,过点P且平行于x轴的直线分别交函数
(2013•海门市二模)如图,点P在y轴正半轴上运动,点C在x轴上运动,过点P且平行于x轴的直线分别交函数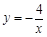 和
和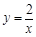 于A、B两点,则△ABC的面积等于
于A、B两点,则△ABC的面积等于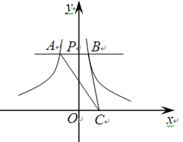
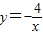 和
和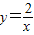 于A、B两点,则三角形ABC的面积等于( )
于A、B两点,则三角形ABC的面积等于( )
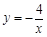 和
和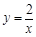 于A、B两点,则△ABC的面积等于
于A、B两点,则△ABC的面积等于