题目内容
18.关于x的方程(k-1)x2-x+1=0有实根.(1)求k 的取值范围;
(2)设x1、x2是方程的两个实数根,且满足(x1+1)(x2+1)=k-1,求实数k的值.
分析 (1)根据方程是一元一次方程和一元二次方程两种情况解答;
(2)根据根与系数的关系,以及(x1+1)(x2+1)=k-1得方程即可求解.
解答 解:(1)∵关于x的方程(k-1)x2-kx+1=0有实根,
∴①方程为一元二次方程时,△≥0且k-1≠0,
即(-1)2-4(k-1)≥0,k≠1,
∴k≤$\frac{5}{4}$且k≠1.
②当方程为一元一次方程时,k-1=0,k=1,
综上,k≤0时方程有实根;
(2)∵x1、x2是方程的两个实数根,
∴x1+x2=$\frac{1}{k-1}$,x1x2=$\frac{1}{k-1}$,
∵(x1+1)(x2+1)=k-1,
∴x1x2+x1+x2+1=k-1,
∴$\frac{1}{k-1}$+$\frac{1}{k-1}$+1=k-1,
解得:k=3或k=0,
∵k≤$\frac{5}{4}$且k≠1.
∴k=0.
点评 本题考查了根与系数的关系,一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
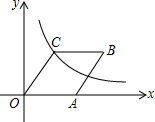 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴的正半轴上,反比例函数y=$\frac{12}{x}$的图象经过点C(3,m).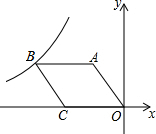 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B.
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B.