题目内容
关于x的一元二次方程(a2-1)x2-(a+1)x+1=0的两根互为倒数,则a的值为( )
A、
| ||
B、-
| ||
C、±
| ||
| D、±2 |
考点:根与系数的关系,一元二次方程的定义
专题:计算题
分析:根据根与系数的关系得到
=1,解得a=±
,然后利用根的判别式确定a的值.
| 1 |
| a2-1 |
| 2 |
解答:解:根据题意得a2-1≠0,即a≠1且a≠-1,
∵方程(a2-1)x2-(a+1)x+1=0的两根互为倒数,
∴
=1,解得a=±
,
∵当a=-
时,方程为x2+(
-1)x+1=0,△=(
-1)2-4<0,此方程没有实数解,
∴a的值为
.
故选A.
∵方程(a2-1)x2-(a+1)x+1=0的两根互为倒数,
∴
| 1 |
| a2-1 |
| 2 |
∵当a=-
| 2 |
| 2 |
| 2 |
∴a的值为
| 2 |
故选A.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.也考查了根的判别式.
| b |
| a |
| c |
| a |

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
下列运算正确的是( )
| A、(3xy2)2=6x2y4 | ||
B、2x-2=
| ||
| C、(-x)7÷(-x)2=-x5 | ||
| D、(6x2)2÷3xy=2xy3 |
在平面直角坐标系中,点P的坐标为(4,-6),则点P在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
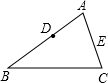 如图,在△ABC中,AB=12,AC=10,点D在AB上,且AD=4,在AC上取一点E,连结DE,使△ADE与原三角形相似.求AE的长.
如图,在△ABC中,AB=12,AC=10,点D在AB上,且AD=4,在AC上取一点E,连结DE,使△ADE与原三角形相似.求AE的长. 如图,P是菱形ABCD对角线BD上一点,PE⊥AB于如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是
如图,P是菱形ABCD对角线BD上一点,PE⊥AB于如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是