题目内容
7.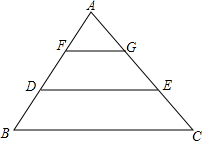 已知,如图,在△ABC中,FG∥DE∥BC,且BD=DF=FA.
已知,如图,在△ABC中,FG∥DE∥BC,且BD=DF=FA.求证:DE+FG=BC.
分析 根据平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例,由FG∥BC得到$\frac{FG}{BC}$=$\frac{AF}{AB}$=$\frac{1}{3}$,由DE∥BC得到$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,即DE=$\frac{2}{3}$BC,所以DE+FG=$\frac{2}{3}$BC+$\frac{1}{3}$BC=BC.
解答 证明:∵FG∥BC,
∴$\frac{FG}{BC}$=$\frac{AF}{AB}$,
而BD=DF=AF,
∴$\frac{FG}{BC}$=$\frac{1}{3}$,即FG=$\frac{1}{3}$BC,
∵DE∥BC,
∴$\frac{DE}{BC}$=$\frac{AD}{AB}$=$\frac{2}{3}$,即DE=$\frac{2}{3}$BC,
∴DE+FG=$\frac{2}{3}$BC+$\frac{1}{3}$BC=BC.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
15.一辆汽车在a s内行驶m m,则它在2min内行驶的路程为( )
| A. | $\frac{m}{3}$m | B. | $\frac{20m}{a}$m | C. | $\frac{10a}{a}$m | D. | $\frac{120m}{a}$m |

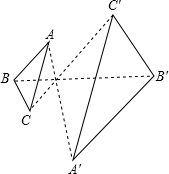 如图,已知△ABC与△A′B′C′是位似图形,求证:AB∥A′B′.
如图,已知△ABC与△A′B′C′是位似图形,求证:AB∥A′B′.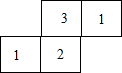 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.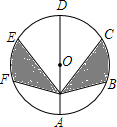 如图所示,AD是⊙O的直径,A,B,C,D,E,F顺次六等分⊙O,已知⊙O的半径为1,P为直径AD上任意一点,求图中阴影部分的面积.
如图所示,AD是⊙O的直径,A,B,C,D,E,F顺次六等分⊙O,已知⊙O的半径为1,P为直径AD上任意一点,求图中阴影部分的面积.