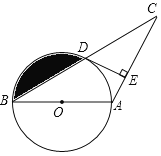
题目内容
【题目】在![]() 中,
中,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,![]() ,与
,与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)由DE⊥BC,D是BC的中点,根据线段垂直平分线的性质,可得BE=CE,又由AD=AC,易得![]() ,
,![]() ,即可证得△ABC∽△FCD;
,即可证得△ABC∽△FCD;
(2)首先过A作AH⊥CD,垂足为H,易得△BDE∽△BHA,可求得AH的长,继而求得△ABC的面积,然后由相似三角形面积比等于相似比的平方,求得△FCD的面积.
(1)证明:∵![]() ,
,![]()
∵![]() 且
且![]() 是
是![]() 的中点
的中点
∴![]()
∴![]()
∴![]()
(2)解:过A作AH⊥CD,垂足为H.
∵AD=AC,
∴DH=CH,
∴BD:BH=2:3,
∵ED⊥BC,
∴ED∥AH,
∴△BDE∽△BHA,
∴ED:AH=BD:BH=2:3,
∵DE=3,
∴AH=![]() ,
,
∵△ABC∽△FCD,BC=2CD,
∴ .
.
∵S△ABC=![]() ×BC×AH=
×BC×AH=![]() ×8×
×8×![]() =18,
=18,
∴S△FCD=![]() S△ABC=
S△ABC=![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目