题目内容
若函数y=ax2+3x+1的图象与x轴有两个交点，求a的取值范围．
分析：因为函数图象和x轴有两个交点，由此可判断此函数为二次函数，进而可得出判别式△＞0，从而得出a的取值范围．
解答：解：∵二次函数y=ax2+3x+1与x轴有两个交点，
∴此函数为二次函数，
∴a≠0，
∴△=b2-4ac=9-4a＞0，
即a＜
，
故a的取值范围是a＜
且a≠0．
∴此函数为二次函数，
∴a≠0，
∴△=b2-4ac=9-4a＞0，
即a＜
| 9 |
| 4 |
故a的取值范围是a＜
| 9 |
| 4 |
点评：本题考查了抛物线和x轴的交点问题，当抛物线和x轴有两个交点时，一元二次方程的判别式大于0，当抛物线和x轴有一个交点时，一元二次方程的判别式等于0，当抛物线和x轴无交点时，一元二次方程的判别式小于0．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
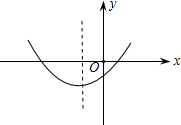若函数y=ax2+bx+c的图象如图所示，则一次函数y=ax+b的图象不经过第
时，二次函数y=ax2+bx+c取得最值
，且函数图象过点A（0，1）．