Question

已知当x=

3

2

时，二次函数y=ax²+bx+c取得最值-

5

4

，且函数图象过点A（0，1）．
（1）求a，b，c的值；
（2）把函数y=ax²+bx+c图象向左平移d个单位后所得函数图象的解析式是y=ax²+x+e，试求e的值；
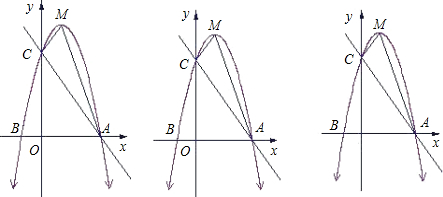
（3）若函数y=ax²+x+e的图象与x轴交于两点A（α，0），B（β，0），且A点在B点左边，试求2α⁴-α³+α²+3α-5的值．

Answer 1

分析：（1）由当x=

3

2

时，二次函数y=ax²+bx+c取得最值-

5

4

，即可得y=ax²+bx+c=a（x-

3

2

）²-

5

4

，又由函数图象过点A（0，1），利用待定系数法即可求得此二次函数的解析式，即可求得a，b，c的值；
（2）由函数y=ax²+bx+c图象向左平移d个单位后所得函数图象的解析式是y=ax²+x+e，即可知平移后，函数图象的顶点是（

3

2

-d，-

5

4

），然后可得顶点式，再整理成一般式，根据多项式相等的知识，即可求得e的值；
（3）由函数y=ax²+x+e的图象与x轴交于两点A（α，0），B（β，0），且A点在B点左边，即可得α是方程x²+x-1=0的较小根，继而求得：α²=1-α与α的值，然后化简2α⁴-α³+α²+3α-5，再代入α的值即可求得答案．

解答：解：（1）∵当x=

3

2

时，二次函数y=ax²+bx+c取得最值-

5

4

，
∴y=ax²+bx+c=a（x-

3

2

）²-

5

4

，
∵图象过点A（0，1）得：

9

4

a-

5

4

=1．
∴a=1．…（2分）
∴y=（x-

3

2

）²-

5

4

=x²-3x+1，
∴a=1，b=-3，c=1．

（2）平移后，函数图象的顶点是（

3

2

-d，-

5

4

）．
函数式为：y=（x-

3

2

+d）²-

5

4

=x²+（2d-3）x+d²-3d+1，
∵函数图象的解析式是y=ax²+x+e，
∴2d-3=1，e=d²-3d+1，
解得d=2，e=-1．

（3）∴y=ax²+x+e=x²+x-1，
∵函数y=ax²+x+e的图象与x轴交于两点A（α，0），B（β，0），且A点在B点左边，
∴α是方程x²+x-1=0的较小根．
∴α²=1-α，且α=

-1- 5

2

． 
∴2α⁴-α³+α²+3α-5=2（1-α）²-α（1-α）+1-α+3α-5
=3a²-3a-2
=1-6a
=4+3

5

点评：此题考查了二次函数的顶点式与一般式的转化，点与函数的关系，待定系数法求函数的解析式等知识．此题综合性较强，难度较大，解题的关键是方程思想与整体思想的应用．