题目内容
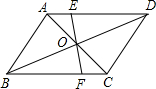 如图,在?ABCD中,对角线AC、BD交于点O,过点O的直线分别交BC、AD于F、E.若AB=4cm,AD=6cm,OE=2cm,则图形EFCD的周长是( )
如图,在?ABCD中,对角线AC、BD交于点O,过点O的直线分别交BC、AD于F、E.若AB=4cm,AD=6cm,OE=2cm,则图形EFCD的周长是( )| A、16cm | B、15cm |
| C、14cm | D、12cm |
考点:平行四边形的性质
专题:
分析:根据平行四边形的对边相等得:CD=AB=4cm,AD=BC=6cm.再根据平行四边形的性质和对顶角相等可以证明:△AOE≌△COF.根据全等三角形的性质,得:OF=OE=2cm,CF=AE,故四边形EFCD的周长为CD+EF+AD=14cm.
解答:解:∵四边形ABCD是平行四边形,
∴CD=AB=4cm,AD=BC=6cm,OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中
∴△AOE≌△COF(AAS).
∴OF=OE=2cm,CF=AE.
故四边形EFCD的周长为CD+EF+AD=14(cm).
故选:C.
∴CD=AB=4cm,AD=BC=6cm,OA=OC,AD∥BC,
∴∠EAO=∠FCO,
在△AOE和△COF中
|
∴△AOE≌△COF(AAS).
∴OF=OE=2cm,CF=AE.
故四边形EFCD的周长为CD+EF+AD=14(cm).
故选:C.
点评:本题考查了平行四边形的性质和全等三角形的判定以及全等三角形的性质,能够根据平行四边形的性质证明三角形全等,再根据全等三角形的性质将所求的线段转化为已知的线段是解题的关键.

练习册系列答案
相关题目
 如图,四个边长为2的小正方形拼成一个大正方形,P是⊙O上的点,OA、OB为半径,则∠APB等于( )
如图,四个边长为2的小正方形拼成一个大正方形,P是⊙O上的点,OA、OB为半径,则∠APB等于( )| A、90° | B、60° |
| C、45° | D、30° |
下列数中,绝对值最大的是( )
A、
| ||
| B、0 | ||
| C、-2 | ||
| D、-1 |
不等式组的解集
在如图中表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
下列命题是假命题的是( )
| A、同旁内角互补 |
| B、垂直于同一条直线的两条直线平行 |
| C、对顶角相等 |
| D、同角的余角相等 |
已知|a-6|+
+(c-10)2=0,则这个三角形的形状是( )
| b-8 |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
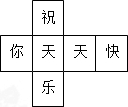 一个材质均匀的正方体的六个面上分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图.随机抛掷这个正方体,结果“天”字朝上的概率是( )
一个材质均匀的正方体的六个面上分别标有文字“祝、你、天、天、快、乐”,其表面展开图如图.随机抛掷这个正方体,结果“天”字朝上的概率是( ) 如图,过y轴上点A的一次函数y=ax+b与反比例函数y=
如图,过y轴上点A的一次函数y=ax+b与反比例函数y=