题目内容
13.函数y=(m-2)x2n+1-m+n,当m=0,n=0时为正比例函数;将点A(4$\sqrt{2}$,0)绕着原点顺时针方向旋转45°角得到点B,则点B的坐标是(4,-4).分析 ①根据正比例函数的定义,转化为关于m、n的方程解答即可.
②由题意可知,A($\sqrt{2}$,0).绕着原点顺时针方向旋转45°得B,我们可以用作图法来完成,过B作BC⊥x轴,知△OBC是等腰直角三角形,根据勾股定理,BC=OC=4,又因为点B在第四象限,故B(4,-4).
解答 解:①∵函数y=(m-2)x2n+1-m+n是正比例函数,
∴$\left\{\begin{array}{l}{m-2≠0}\\{2n+1=1}\\{-m+n=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=0}\\{n=0}\end{array}\right.$;
②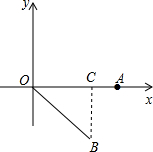 ∵OB=OA=4$\sqrt{2}$,做BC⊥x轴于点C,那么△OBC是等腰直角三角形,
∵OB=OA=4$\sqrt{2}$,做BC⊥x轴于点C,那么△OBC是等腰直角三角形,
∴OC=BC=4,
∵在第四象限,
∴点B的坐标是(4,-4).
故答案为0,0,(4,-4).
点评 本题主要考查了正比例函数的定义,也考查了旋转问题,掌握数形结合的数学思想是解决问题的关键.

练习册系列答案
相关题目
2.抛物线y=ax2经过点(1,3),则a的值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 9 |
3.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)中,x与y的部分对应值如下表:
有下列结论:
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -3.5 | -1 | 0.5 | 1 | 0.5 | -1 | -3.5 | … |
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
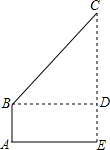 如图,小芳站在地面上A处放风筝,风筝飞到C处时的线长BC为23米,这时测得∠CBD=58°,牵引底端B与地面的距离BA为1.6米,求此时风筝离地面的高度CE.(结果精确到0.1米)(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)
如图,小芳站在地面上A处放风筝,风筝飞到C处时的线长BC为23米,这时测得∠CBD=58°,牵引底端B与地面的距离BA为1.6米,求此时风筝离地面的高度CE.(结果精确到0.1米)(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60)