题目内容
已知矩形ABCD,AB=6,BC=10,将矩形ABCD沿着过点C的直线折叠使得点B落到直线AD上的点B′处,设折痕所在直线与直线AD相交于点E,则tan∠CED= .
考点:翻折变换(折叠问题)
专题:
分析:如图1、2,首先根据题意作出两种符合题意的几何图形;在图1中,根据勾股定理求出DB′的长度;证明B′E=BC,问题即可解决.
解答: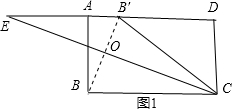 解:如图1,
解:如图1,
当点B′在边AD上时,连接BB′,交EC于点O;
由题意得:EC⊥BB′,且平分BB′,
∴B′C=BC=10,BO=BO′;
∵四边形ABCD为矩形,
∴∠D=90°,DC=AB=6;
由勾股定理得:
B′D2=B′C2-DC2=100-36=64,
∴B′D=8;
∵四边形ABCD为矩形,
∴DE∥BC,
∴∠E=∠BCO;
在△EOB′与△COB中,
,
∴△EOB′≌△COB(AAS),
∴B′E=B′C=10,
∴ED=10+8=18,
tan∠CED=
=
=
,
故该题答案为
.
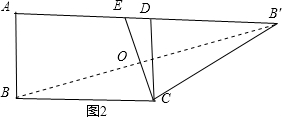 如图2,若点B′在直线AD上时,
如图2,若点B′在直线AD上时,
连接BB′,交EC于点O;
类比上述解法,同理可求:
B′D=8,B′E=BC=10,
∴DE=10-8=2,
∴tan∠CED=
=
=3;
故答案为3.
 解:如图1,
解:如图1,当点B′在边AD上时,连接BB′,交EC于点O;
由题意得:EC⊥BB′,且平分BB′,
∴B′C=BC=10,BO=BO′;
∵四边形ABCD为矩形,
∴∠D=90°,DC=AB=6;
由勾股定理得:
B′D2=B′C2-DC2=100-36=64,
∴B′D=8;
∵四边形ABCD为矩形,
∴DE∥BC,
∴∠E=∠BCO;
在△EOB′与△COB中,
|
∴△EOB′≌△COB(AAS),
∴B′E=B′C=10,
∴ED=10+8=18,
tan∠CED=
| CD |
| ED |
| 6 |
| 18 |
| 1 |
| 3 |
故该题答案为
| 1 |
| 3 |
 如图2,若点B′在直线AD上时,
如图2,若点B′在直线AD上时,连接BB′,交EC于点O;
类比上述解法,同理可求:
B′D=8,B′E=BC=10,
∴DE=10-8=2,
∴tan∠CED=
| CD |
| DE |
| 6 |
| 2 |
故答案为3.
点评:该命题以矩形为载体,以翻折变换为方法,在考查了翻折变换的性质及其应用的同时,还渗透了勾股定理、全等三角形的判定及其应用等重要几何知识点的考查;运用分类讨论的数学思想作出两种符合题意的几何图形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AD∥BE∥CF,直线a、b与这三条平行线分别交于点A、B、C和点D、E、F,AB=4,BC=6,DE=3,则EF的长是( )
如图,AD∥BE∥CF,直线a、b与这三条平行线分别交于点A、B、C和点D、E、F,AB=4,BC=6,DE=3,则EF的长是( ) 如图,已知点P是半径为1.5的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=2,则?ABCD面积的最大值为
如图,已知点P是半径为1.5的⊙A上一点,延长AP到C,使PC=AP,以AC为对角线作?ABCD.若AB=2,则?ABCD面积的最大值为