ÌâÄżÄÚÈĘ
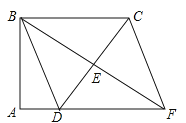
ĄŸÌâÄżĄżÈçÍŒ1ŁŹÔÚÒ»ŐĆł€·œĐÎÖœÌőÉϻһÌőÊęÖᣟ

Łš1Ł©ÈôŐÛ”țÖœÌőÊčÊęÖáÉϱíÊŸ©1”Ä”ăÓë±íÊŸ5”Ä”ăÖŰșÏŁŹÔòŐÛșÛÓëÊęÖá”Äœ»”ă±íÊŸ”ÄÊęÊÇĄĄ ĄĄŁ»
Łš2Ł©ÈçčûÊęÖáÉÏÁœ”ăÖźŒä”ÄŸàÀëÎȘ6+m2ŁšmÎȘłŁÊ꣩ŁŹŐâÁœ”ăŸč꣚1Ł©”ÄŐÛ”ț·œÊœșóŐÛșÛÓëÊęÖá”Äœ»”ăÓ룚1Ł©ÖĐ”Äœ»”ăÏàÍŹŁŹÇóŚó±ßŐâžö”ă±íÊŸ”ÄÊꣻŁšÓĂșŹm”ÄŽúÊęÊœ±íÊŸŁ©
Łš3Ł©ÈçÍŒ2ŁŹÈôœ«ŽËÖœÌőŃŰAŁŹBŽŠŒôżȘŁŹœ«ÖĐŒä”ÄÒ»¶ÎÖœÌő¶ÔŐÛŁŹÊčÆäŚóÓÒÁœ¶ËÖŰșÏŁŹŐâŃùÁŹĐű¶ÔŐÛnŽÎșóŁŹÔÙœ«ÆäŐčżȘŁŹÇóŚîÓҶ˔ÄŐÛșÛÓëÊęÖá”Äœ»”ă±íÊŸ”ÄÊ꣟ŁšÓĂșŹn”ÄŽúÊęÊœ±íÊŸŁ©
ĄŸŽđ°žĄżŁš1Ł©2Ł»Łš2Ł©©1©![]() Ł»Łš3Ł© 4©
Ł»Łš3Ł© 4©![]()
ĄŸœâÎöĄż
Łš1Ł©”ă©1Óë5ÊÇ¶ÔłÆ”ÄŁŹœ»”ăÎȘ2Ł»
Łš2Ł©ÉèÁœžö”ăŚó±ß”ÄÎȘxŁŹÓұߔÄÎȘyŁŹy©xŁœ6+m2ŁŹx+yŁœ4ŁŹÇółöxŒŽżÉŁ»
Łš3Ł©¶ÔŐÛnŽÎșóŁŹĂżÁœÌőÏàÁÚŐÛșÛŒä”ÄŸàÀë![]() Łœ
Łœ![]() ŁŹŚîÓҶ˔ÄŐÛșÛÓëÊęÖá”Äœ»”ă±íÊŸ”ÄÊęÎȘ4©
ŁŹŚîÓҶ˔ÄŐÛșÛÓëÊęÖá”Äœ»”ă±íÊŸ”ÄÊęÎȘ4©![]() Łź
Łź
œâŁșŁš1Ł©ÓÉŐÛ”țʱŁŹ”ă©1Óë5ÊÇ¶ÔłÆ”ÄŁŹ
Ąà©1șÍ5”ÄÖĐ”ăÎȘŐÛșÛÓëÊęÖá”Äœ»”㣏
Ąàœ»”ăÎȘ2ŁŹ
čÊŽđ°žÎȘ2Ł»
Łš2Ł©ÉèÁœžö”ăŚó±ß”ÄÎȘxŁŹÓұߔÄÎȘyŁŹ
ĄßÁœ”ăÖźŒä”ÄŸàÀëÎȘ6+m2ŁŹ
Ąày©xŁœ6+m2ŁŹ
ÓÉŁš1Ł©ÖȘœ»”ăÎȘ2ŁŹ
Ąàx+yŁœ4ŁŹ
ĄàxŁœ©1©![]() ŁŹ
ŁŹ
ĄàŚó±ß”ÄŐâžö”ă±íÊŸ”ÄÊęÊÇ©1©![]() Łź
Łź
Łš3Ł©¶ÔŐÛnŽÎșóŁŹĂżÁœÌőÏàÁÚŐÛșÛŒä”ÄŸàÀë![]() Łœ
Łœ![]() ŁŹ
ŁŹ
ĄàŚîÓҶ˔ÄŐÛșÛÓëÊęÖá”Äœ»”ă±íÊŸ”ÄÊęÎȘ4©![]() Łź
Łź

 »îÁŠżÎÊ±ÍŹČœÁ·Ï°ČáÏ”ÁĐŽđ°ž
»îÁŠżÎÊ±ÍŹČœÁ·Ï°ČáÏ”ÁĐŽđ°ž Ń§Ò”ČâÆÀÒ»żÎÒ»ČâÏ”ÁĐŽđ°ž
Ń§Ò”ČâÆÀÒ»żÎÒ»ČâÏ”ÁЎ𰞥ŸÌâÄżĄżÄłÉÌłĄ·țŚ°ČżÎȘÁË”ś¶ŻÓȘÒ”Ô±”Ä»ęŒ«ĐÔŁŹŸö¶šÊ”ĐĐÄż±êčÜÀíŁŹžùŸĘÄż±êÍêłÉ”ÄÇéżö¶ÔÓȘÒ”Ô±œűĐĐÊÊ”±”Äœ±ÀűŁźÎȘÁËÈ·¶šÒ»žöÊÊ”±”ÄÔÂÏúÊÛÄż±êŁŹÉÌłĄ·țŚ°ČżÍłŒÆÁËÿλÓȘÒ”Ô±ÔÚÄłÔ”ÄÏúÊÛ¶îŁš”„λŁșÍòÔȘŁ©ŁŹÊęŸĘÈçÏÂŁș
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
¶ÔŐâ30žöÊęŸĘ°ŽŚéŸà3œűĐз֌飏ȹŐûÀíĄąĂèÊöșÍ·ÖÎöÈçÏÂŁź
Æ”Êę·ÖČŒ±í
Śé±đ | Ò» | ¶ț | Èę | ËÄ | Îć | Áù | Æß |
ÏúÊÛ¶î |
|
|
|
|
|
|
|
Æ”Êę | 7 | 9 | 3 |
| 2 |
| 2 |
ÊęŸĘ·ÖÎö±í
ÆœŸùÊę | ÖÚÊę | ÖĐλÊę |
20.3 |
| 18 |
ÇëžùŸĘÒÔÉÏĐĆÏąœâŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©ÌîżŐŁșa=ĄĄĄĄŁŹb=ĄĄĄĄŁŹc=ĄĄĄĄŁ»
Łš2Ł©Èôœ«ÔÂÏúÊÛ¶îČ»”ÍÓÚ25ÍòÔȘÈ·¶šÎȘÏúÊÛÄż±êŁŹÔòÓĐĄĄĄĄÎ»ÓȘÒ”Ô±»ń”Ăœ±ÀűŁ»
Łš3Ł©ÈôÏëÈĂÒ»°ëŚóÓÒ”ÄÓȘÒ”Ô±¶ŒÄ܎ÏúÊÛÄż±êŁŹÄăÈÏÎȘÔÂÏúÊ۶ÎȘ¶àÉÙșÏÊÊŁżË”ĂśÀíÓÉŁź