题目内容
 如图,在△ABC中,AB=AC=4
如图,在△ABC中,AB=AC=4| 2 |
(1)当⊙P与直线AC相切时,求t的值;
(2)当⊙P与⊙A相切时,求t的值;
(3)延长BA交⊙A于点D,连接AP交⊙A于点E,连接DE并延长交BC于点F.当△ABP与△FBD相似时,求t的值.
考点:圆的综合题
专题:
分析:(1)过点P作PK⊥AC,垂足为点K,根据⊙P与直线AC相切可知BP=PK=t.故可得出△ABC是等腰直角三角形,△PKC是等腰直角三角形,故PC=
PK=
t,由此可得出t的值;
(2)过点A作AM⊥BC,垂足为点M,故AP2=AM2+PM2,AM=
BC=4,PM=t-4或4-t,再根据⊙P与⊙A外切,⊙P与⊙A内切两种情况即可得出t的值;
(3)当△ABP∽△FBD时,∠D=∠BPA,根据∠D=∠AED=∠FEP可得∠D=∠AED=∠FEP=∠BPA,故∠BFD=2∠D,根据三角形内角和定理可求出∠D的度数,故可得出结论.
| 2 |
| 2 |
(2)过点A作AM⊥BC,垂足为点M,故AP2=AM2+PM2,AM=
| 1 |
| 2 |
(3)当△ABP∽△FBD时,∠D=∠BPA,根据∠D=∠AED=∠FEP可得∠D=∠AED=∠FEP=∠BPA,故∠BFD=2∠D,根据三角形内角和定理可求出∠D的度数,故可得出结论.
解答: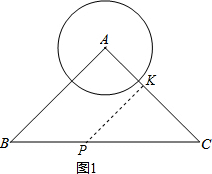 解:(1)如图1,过点P作PK⊥AC,垂足为点K,
解:(1)如图1,过点P作PK⊥AC,垂足为点K,
∵⊙P与直线AC相切,
∴BP=PK=t.
∵AB=AC=4
,BC=8,
∴△ABC是等腰直角三角形,
∴∠C=45°,
∴△PKC是等腰直角三角形.
∴PC=
PK=
t,
∴t+
t=8.
解得t=8
-8;
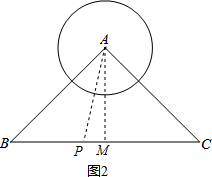
(2)如图2,过点A作AM⊥BC,垂足为点M,则AP2=AM2+PM2,
AM=
BC=4,PM=t-4或4-t,
若⊙P与⊙A外切,则(t+2)2=42+(t-4)2,
解得t=
.
若⊙P与⊙A内切,则(t-2)2=42+(t-4)2,
解得t=7.
综上所述,当t=
或t=7时,⊙P与⊙A相切.
(3)当△ABP∽△FBD时,∠D=∠BPA,
 ∵∠D=∠AED=∠FEP,
∵∠D=∠AED=∠FEP,
∴∠D=∠AED=∠FEP=∠BPA.
∴∠BFD=2∠D.
∵∠D+∠B+∠BFD=180°,
∴∠D=45°,
∴∠BAP=90°.
∴AP与AC重合,
∴t=8.
 解:(1)如图1,过点P作PK⊥AC,垂足为点K,
解:(1)如图1,过点P作PK⊥AC,垂足为点K,∵⊙P与直线AC相切,
∴BP=PK=t.
∵AB=AC=4
| 2 |
∴△ABC是等腰直角三角形,
∴∠C=45°,
∴△PKC是等腰直角三角形.
∴PC=
| 2 |
| 2 |
∴t+
| 2 |
解得t=8
| 2 |

(2)如图2,过点A作AM⊥BC,垂足为点M,则AP2=AM2+PM2,
AM=
| 1 |
| 2 |
若⊙P与⊙A外切,则(t+2)2=42+(t-4)2,
解得t=
| 7 |
| 3 |
若⊙P与⊙A内切,则(t-2)2=42+(t-4)2,
解得t=7.
综上所述,当t=
| 7 |
| 3 |
(3)当△ABP∽△FBD时,∠D=∠BPA,
 ∵∠D=∠AED=∠FEP,
∵∠D=∠AED=∠FEP,∴∠D=∠AED=∠FEP=∠BPA.
∴∠BFD=2∠D.
∵∠D+∠B+∠BFD=180°,
∴∠D=45°,
∴∠BAP=90°.
∴AP与AC重合,
∴t=8.
点评:本题考查的是圆的综合题,涉及到切线的性质、相似三角形的判定与性质、等腰直角三角形的判定与性质等知识,难度较大.

练习册系列答案
相关题目
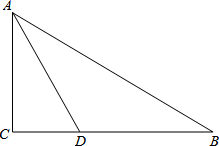 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线. 如图,直线l:y=
如图,直线l:y=