题目内容
2.已知关于x的方程m=2x-5的解满足$\left\{\begin{array}{l}{x-y=6-n}\\{x+2y=5n}\end{array}\right.$(0<n<4),若y≥2,则m的取值范围是7≤m<11.分析 表示出已知方程的解得到x,由方程组变形表示出x,y,两者相等列出m与n的关系式,根据y的范围求出n的范围,继而求出m的范围.
解答 解:方程m=2x-5,解得:x=$\frac{m+5}{2}$,
方程组$\left\{\begin{array}{l}{x-y=6-n}\\{x+2y=5n}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=n+4}\\{y=2n-2}\end{array}\right.$,
可得$\frac{m+5}{2}$=n+4,即n=$\frac{m+5}{2}$-4,
由y≥2,得到2n-2≥2,
解得:n≥2,即4>$\frac{m+5}{2}$-4≥2,
整理得:m+5≥12且m+5<16,
解得:7≤m<11,
故答案为:7≤m<11
点评 此题考查了解一元一次不等式,以及二元一次方程组的解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.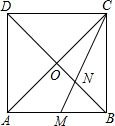 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )
 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )
如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB、BD于M、N两点,若AM=4,则线段ON的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |
17.如图①是正方体的展开图,如果将其折成原来的正方体(如图②),那么与点M重合的两点应该是( )


| A. | S和Z | B. | W和Y | C. | U和Y | D. | T和V |
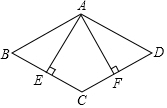 如图,在菱形ABCD中,E,F分别为BC,CD的中点,且AE⊥BC,AF⊥CD,垂足分别为E,F.求∠EAF的度数.
如图,在菱形ABCD中,E,F分别为BC,CD的中点,且AE⊥BC,AF⊥CD,垂足分别为E,F.求∠EAF的度数.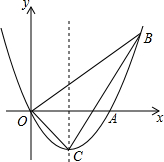 如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.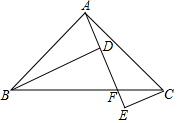 如图,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,AE与BC交于F点.
如图,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,AE与BC交于F点.