题目内容

如图，将正五边形ABCDE绕C点顺时针方向旋转，则旋转n度后使得新五边形A′B′C′D′E′的顶点D′第一次落在直线BC上，则n的值是（　　）
分析：先根据多边形外角和定理得到正五边形的每个外角的度数=
360°
5
=72°，根据旋转的性质将正五边形ABCDE绕C点顺时针方向旋转后所得新五边形A′B′C′D′E′的顶点D′第一次落在直线BC上
则旋转角应为72°．
解答：解：∵正五边形的每个外角的度数=
360°
5
=72°，
∴将正五边形ABCDE绕C点顺时针方向旋转72°时，所得新五边形A′B′C′D′E′的顶点D′第一次落在直线BC上．
故选B．
点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．
练习册系列答案
相关题目
有一张矩形纸片ABCD，按下面步骤进行折叠：
第一步：如图①，将矩形纸片ABCD折叠，使点B、D重合，点C落在点C′处，得折痕EF；
第二步：如图②，将五边形AEFC′D折叠，使AE、C′F重合，得折痕DG，再打开；
第三步：如图③，进一步折叠，使AE、C′F均落在DG上，点A、C′落在点A′处，点E、F落在点E′处，得折痕MN、QP．
这样，就可以折出一个五边形DMNPQ．
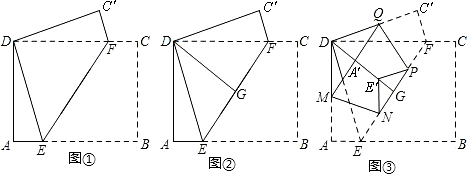
精英家教网
（1）请写出图①中一组相等的线段
 
写出一组即可；
（2）若这样折出的五边形DMNPQ，如图③，恰好是一个正五边形，当AB=a，AD=b，DM=m时，有下列结论：
①a2-b2=2abtan18°；②m=
a2+b2
•tan18°；
③b=m+atan18°；④b=
3
2
m+mtan18°．
其中，正确结论的序号是
 
把你认为正确结论的序号都填上．

有一张矩形纸片ABCD，按下面步骤进行折叠：
第一步：如图①，将矩形纸片ABCD折叠，使点B、D重合，点C落在点处，得折痕EF；
第二步：如图②，将五边形折叠，使AE、重合，得折痕DG，再打开；
第三步：如图③，进一步折叠，使AE、均落在DG上，点A、落在点处，点E、F落在点处，得折痕MN、QP.这样，就可以折出一个五边形DMNPQ.

（Ⅰ）请写出图①中一组相等的线段                （写出一组即可）；
（Ⅱ）若这样折出的五边形DMNPQ（如图③）恰好是一个正五边形，当AB=a，AD=b，DM=m时，有下列结论：
①；         ②；
③；           ④.
其中，正确结论的序号是             （把你认为正确结论的序号都填上）.

有一张矩形纸片ABCD，按下面步骤进行折叠：

第一步：如图①，将矩形纸片ABCD折叠，使点B、D重合，点C落在点处，得折痕EF；

第二步：如图②，将五边形折叠，使AE、重合，得折痕DG，再打开；

第三步：如图③，进一步折叠，使AE、均落在DG上，点A、落在点处，点E、F落在点处，得折痕MN、QP.这样，就可以折出一个五边形DMNPQ.

（Ⅰ）请写出图①中一组相等的线段                 （写出一组即可）；

（Ⅱ）若这样折出的五边形DMNPQ（如图③）恰好是一个正五边形，当AB=a，AD=b，DM=m时，有下列结论：

①；          ②；

③；            ④.

其中，正确结论的序号是              （把你认为正确结论的序号都填上）.

 
（2010•天津）有一张矩形纸片ABCD，按下面步骤进行折叠：
第一步：如图①，将矩形纸片ABCD折叠，使点B、D重合，点C落在点C′处，得折痕EF；
第二步：如图②，将五边形AEFC′D折叠，使AE、C′F重合，得折痕DG，再打开；
第三步：如图③，进一步折叠，使AE、C′F均落在DG上，点A、C'落在点A'处，点E、F落在点E′处，得折痕MN、QP．
这样，就可以折出一个五边形DMNPQ．

（1）请写出图①中一组相等的线段    写出一组即可；
（2）若这样折出的五边形DMNPQ，如图③，恰好是一个正五边形，当AB=a，AD=b，DM=m时，有下列结论：
①a2-b2=2abtan18°；②；
③b=m+atan18°；④．
其中，正确结论的序号是    把你认为正确结论的序号都填上．
（2010•天津）有一张矩形纸片ABCD，按下面步骤进行折叠：
第一步：如图①，将矩形纸片ABCD折叠，使点B、D重合，点C落在点C′处，得折痕EF；
第二步：如图②，将五边形AEFC′D折叠，使AE、C′F重合，得折痕DG，再打开；
第三步：如图③，进一步折叠，使AE、C′F均落在DG上，点A、C'落在点A'处，点E、F落在点E′处，得折痕MN、QP．
这样，就可以折出一个五边形DMNPQ．

（1）请写出图①中一组相等的线段    写出一组即可；
（2）若这样折出的五边形DMNPQ，如图③，恰好是一个正五边形，当AB=a，AD=b，DM=m时，有下列结论：
①a2-b2=2abtan18°；②；
③b=m+atan18°；④．
其中，正确结论的序号是    把你认为正确结论的序号都填上．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网