题目内容
有一张矩形纸片ABCD,按下面步骤进行折叠:第一步:如图①,将矩形纸片ABCD折叠,使点B、D重合,点C落在点C′处,得折痕EF;
第二步:如图②,将五边形AEFC′D折叠,使AE、C′F重合,得折痕DG,再打开;
第三步:如图③,进一步折叠,使AE、C′F均落在DG上,点A、C′落在点A′处,点E、F落在点E′处,得折痕MN、QP.
这样,就可以折出一个五边形DMNPQ.
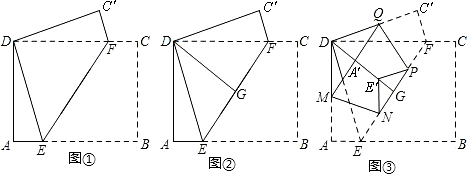
(1)请写出图①中一组相等的线段
(2)若这样折出的五边形DMNPQ,如图③,恰好是一个正五边形,当AB=a,AD=b,DM=m时,有下列结论:
①a2-b2=2abtan18°;②m=
| a2+b2 |
③b=m+atan18°;④b=
| 3 |
| 2 |
其中,正确结论的序号是
分析:(1)由翻折的性质知:C′D与CD是对应线段,而AB=CD,故有AD=C′D;
(2)由题意知点G是矩形的中心,即延长DG过B点,延长MN也过点B,可得∠DBM=∠ABM=∠ADE=18°,然后分析四个结论.
(2)由题意知点G是矩形的中心,即延长DG过B点,延长MN也过点B,可得∠DBM=∠ABM=∠ADE=18°,然后分析四个结论.
解答:解:(1)由题意知,C′D与CD是对应线段,而AB=CD,故有AD=C′D;
(2)由题意知点G是矩形的中心,即延长DG过B点,延长MN也过点B,
由于五边形DMNPQ,恰好是一个正五边形,且由折叠的过程知:∠MDB=54°,∠DMB=108°,
∴∠DBM=∠ABM=18°,
∴∠DBA=36°.
∵DE=BE,∠EDB=∠DBA=36°,
∴∠ADE=∠MDB-∠EDB=54°-36°=18°.
在Rt△ADE中,由勾股定理知,AD2+AE2=DE2=BE2,即b2+AE2=(a-AE)2,
解得AE=
.
∵tan∠ADE=tan18°=
=
=
,
∴a2-b2=2abtan18°,即①正确;
∵PN=DM,
∴PG=NG=
PN=
DM=
m,
∵BG=
DB=
,NG=
DM=
m,NG⊥BD,
∴tan∠GBN=tan18°=NG:BG=
m:
.
∴m=
•tan18°,即②正确.
∵AM=AD-DM=b-m,AB=a,
∴tan∠ABM=tan18°=AM:AB=(b-m):a,
∴b=m+atan18°,即③正确,同时④错误.
故①②③正确.
(2)由题意知点G是矩形的中心,即延长DG过B点,延长MN也过点B,
由于五边形DMNPQ,恰好是一个正五边形,且由折叠的过程知:∠MDB=54°,∠DMB=108°,

∴∠DBM=∠ABM=18°,
∴∠DBA=36°.
∵DE=BE,∠EDB=∠DBA=36°,
∴∠ADE=∠MDB-∠EDB=54°-36°=18°.
在Rt△ADE中,由勾股定理知,AD2+AE2=DE2=BE2,即b2+AE2=(a-AE)2,
解得AE=
| a2-b2 |
| 2a |
∵tan∠ADE=tan18°=
| AE |
| AD |
| AE |
| b |
| a2-b2 |
| 2ab |
∴a2-b2=2abtan18°,即①正确;
∵PN=DM,
∴PG=NG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵BG=
| 1 |
| 2 |
| 1 |
| 2 |
| a2+b2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴tan∠GBN=tan18°=NG:BG=
| 1 |
| 2 |
| 1 |
| 2 |
| a2+b2 |
∴m=
| a2+b2 |
∵AM=AD-DM=b-m,AB=a,
∴tan∠ABM=tan18°=AM:AB=(b-m):a,
∴b=m+atan18°,即③正确,同时④错误.
故①②③正确.
点评:本题考查了翻折的性质:对应角相等,对应边相等及正五边形的性质、勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
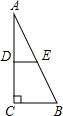 如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
如图,在一张△ABC纸片中,∠C=90°,∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有两个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( ) 如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一




 = ;
= ; 




 = ;
= ; 