题目内容
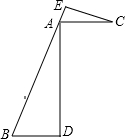 如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条直线上.
如图,AB=3AC,BD=3AE,又BD∥AC,点B,A,E在同一条直线上.(1)求证:△ABD∽△CAE;
(2)如果AC=BD,AD=2
| 2 |
分析:(1)由BD∥AC,得∠EAC=∠B;根据已知条件,易证得AB:AC和BD:AE的值相等,由此可根据SAS判定两个三角形相似.
(2)首先根据已知条件表示出AB、AD、AC的值,进而可由勾股定理判定∠D=∠E=90°;根据(1)得出的相似三角形的相似比,可表示出EC、AE的长,进而可在Rt△BEC中,根据勾股定理求出BC的长.
(2)首先根据已知条件表示出AB、AD、AC的值,进而可由勾股定理判定∠D=∠E=90°;根据(1)得出的相似三角形的相似比,可表示出EC、AE的长,进而可在Rt△BEC中,根据勾股定理求出BC的长.
解答: (1)证明:∵BD∥AC,点B,A,E在同一条直线上,
(1)证明:∵BD∥AC,点B,A,E在同一条直线上,
∴∠DBA=∠CAE,
又∵
=
=3,
∴△ABD∽△CAE;(4分)
(2)连接BC,
解:∵AB=3AC=3BD,AD=2
BD,
∴AD2+BD2=8BD2+BD2=9BD2=AB2,
∴∠D=90°,
由(1)得△ABD∽△CAE
∴∠E=∠D=90°,
∵AE=
BD,EC=
AD=
BD,AB=3BD,
∴在Rt△BCE中,BC2=(AB+AE)2+EC2
=(3BD+
BD)2+(
BD)2=
BD2=12a2,
∴BC=2
a.(6分)
 (1)证明:∵BD∥AC,点B,A,E在同一条直线上,
(1)证明:∵BD∥AC,点B,A,E在同一条直线上,∴∠DBA=∠CAE,
又∵
| AB |
| AC |
| BD |
| AE |
∴△ABD∽△CAE;(4分)
(2)连接BC,
解:∵AB=3AC=3BD,AD=2
| 2 |
∴AD2+BD2=8BD2+BD2=9BD2=AB2,
∴∠D=90°,
由(1)得△ABD∽△CAE
∴∠E=∠D=90°,
∵AE=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
∴在Rt△BCE中,BC2=(AB+AE)2+EC2
=(3BD+
| 1 |
| 3 |
2
| ||
| 3 |
| 108 |
| 9 |
∴BC=2
| 3 |
点评:此题主要考查了相似三角形的判定和性质,以及勾股定理的应用.能够由勾股定理判断出△ABD和△AEC是直角三角形,是解答(2)题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
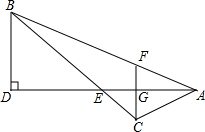 (2011•邢台一模)如图,AB=3AC,AD平分∠BAC,BD⊥AD,BC交AD于点E,CF∥BD.
(2011•邢台一模)如图,AB=3AC,AD平分∠BAC,BD⊥AD,BC交AD于点E,CF∥BD.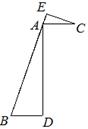
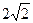 BD,设BD = a,求BC的长.
BD,设BD = a,求BC的长.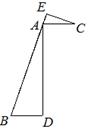
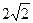 BD,设BD = a,求BC的长.
BD,设BD = a,求BC的长.