Question

(本小题满分10分)
如图，AB = 3AC，BD = 3AE，又BD∥AC，点B，A，E在同一条直线上.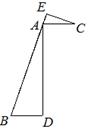

(1) 求证：△ABD∽△CAE；
(2) 如果AC =BD，AD =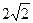BD，设BD = a，求BC的长.

Answer 1

（1）△ABD∽△CAE,证明略。
(2) a

解析(1) ∵ BD∥AC，点B，A，E在同一条直线上，  ∴ÐDBA = ÐCAE,
又∵,
∴ △ABD∽△CAE.       --- 4分
(2)  ∵AB =" 3AC" = 3BD，AD =2BD ，
(第22题)
∴ AD2 + BD2 =" 8BD2" + BD2 =" 9BD2" =AB2，              
∴ÐD ="90°,             "
由（1）得 ÐE =ÐD =" 90°, "
∵ AE=BD , EC =AD = BD , AB =" 3BD" ，
∴在Rt△BCE中，BC2 =" (AB" + AE )2 + EC2
=" (3BD" +BD )2 + (BD)2 = BD2 =" 12a2" ,
∴ BC =a .                                       --- 6分