题目内容
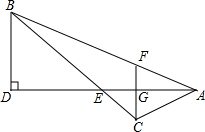（2011•邢台一模）如图，AB=3AC，AD平分∠BAC，BD⊥AD，BC交AD于点E，CF∥BD．（1）求证：△ACG≌△AFG
（2）求
| FG |
| BD |
（3）求
| EG |
| ED |
（4）判断AE和DE之间的数量关系，并说明理由．
分析：（1）根据ASA证明△ACG≌△AFG；
（2）根据CF∥BD可证△AFG∽△ABD，运用相似三角形性质求解；
（3）可证△ECG∽△EBD，得EG：ED=CG：BD=FG：BD；
（4）综合运用上面结论可判定AE=DE．
（2）根据CF∥BD可证△AFG∽△ABD，运用相似三角形性质求解；
（3）可证△ECG∽△EBD，得EG：ED=CG：BD=FG：BD；
（4）综合运用上面结论可判定AE=DE．
解答：（1）证明：∵DA平分∠BAC，
∴∠FAG=∠CAG，
∵BD⊥AD，CF∥BD，
∴CF⊥AD，
∴∠AGF=∠AGC=90°，
在△AFG和△ACG中，
∵∠FAG=∠CAG，AG=AG，∠AGF=∠AGC，
∴△AFG≌△ACG．
（2）解：∵△AFG≌△ACG，
∴AC=AF，CG=FG．
∵CF∥BD，
∴△AFG∽△ABD，
∴
=
=
=
；
（3）解：∵CF∥BD，
∴△ECG∽△EBD，
∴
=
=
=
；
（4）解：AE=DE．
理由：设EG=x，则ED=3x．
=
=
．
解得 AG=2x．
∴AE=3x=DE．
∴∠FAG=∠CAG，
∵BD⊥AD，CF∥BD，
∴CF⊥AD，
∴∠AGF=∠AGC=90°，
在△AFG和△ACG中，
∵∠FAG=∠CAG，AG=AG，∠AGF=∠AGC，
∴△AFG≌△ACG．
（2）解：∵△AFG≌△ACG，
∴AC=AF，CG=FG．
∵CF∥BD，
∴△AFG∽△ABD，
∴
| FG |
| BD |
| AF |
| AB |
| AC |
| AB |
| 1 |
| 3 |
（3）解：∵CF∥BD，
∴△ECG∽△EBD，
∴
| EG |
| ED |
| CG |
| BD |
| FG |
| BD |
| 1 |
| 3 |
（4）解：AE=DE．
理由：设EG=x，则ED=3x．
| AG |
| AD |
| AG |
| AG+4x |
| 1 |
| 3 |
解得 AG=2x．
∴AE=3x=DE．
点评：此题考查相似（包括全等）三角形的判定和性质，综合性较强，难度较大．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
（2011•邢台一模）如图，正方形ABCD边长为2，E为CD的中点，以点A为中心，把△ADE顺时针旋转90°得△ABF，连接EF，则EF的长等于