题目内容
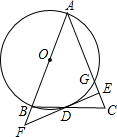 如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,交AC于点G,过点D作DE⊥AC于点E,延长ED交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O交BC于点D,交AC于点G,过点D作DE⊥AC于点E,延长ED交AB的延长线于点F.(1)判断直线EF与⊙O的位置关系,并说明理由.
(2)若AB=13,BC=10.求AE的长.
考点:切线的判定
专题:
分析:(1)首先连接OD,由AB=AC,OB=OD,易得∠ABD=∠ODB=∠C,继而可得OD∥AC,然后由DE⊥AC,证得DE⊥OD,则可得直线EF与⊙O相切.
(2)首先连接AD,由圆周角定理,可得∠ADB=90°,然后由三线合一,可求得BD的长,再由勾股定理,求得AD的长,易证得△AED∽△ADC,然后由相似三角形的对应边成比例,求得答案.
(2)首先连接AD,由圆周角定理,可得∠ADB=90°,然后由三线合一,可求得BD的长,再由勾股定理,求得AD的长,易证得△AED∽△ADC,然后由相似三角形的对应边成比例,求得答案.
解答: 解:(1)直线EF与⊙O相切.
解:(1)直线EF与⊙O相切.
理由:连接OD,
∵AB=AC,OB=OD,
∴∠ABC=∠C,∠OBD=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴直线EF与⊙O相切.
(2)连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=DC=
BC=5,
∴AD=
=
=12,
∵∠DAC=∠DAC,∠ADC=∠AED=90°,
∴△AED∽△ADC,
∴
=
,
即
=
,
解得:AE=
.
 解:(1)直线EF与⊙O相切.
解:(1)直线EF与⊙O相切.理由:连接OD,
∵AB=AC,OB=OD,
∴∠ABC=∠C,∠OBD=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴直线EF与⊙O相切.
(2)连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=DC=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 132-52 |
∵∠DAC=∠DAC,∠ADC=∠AED=90°,
∴△AED∽△ADC,
∴
| AE |
| AD |
| AD |
| AC |
即
| AE |
| 12 |
| 12 |
| 13 |
解得:AE=
| 144 |
| 13 |
点评:此题考查了切线的性质与判定、圆周角定理、等腰三角形的性质、勾股定理以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
矩形具有而一般平行四边形不一定具有的性质是( )
| A、对角线相等 |
| B、对角相等 |
| C、对角线互相平分 |
| D、对边相等 |
 如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB于点D,那么sin∠BCD的值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=12,BC=5,CD⊥AB于点D,那么sin∠BCD的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
下列问题中,适合用普查的是( )
| A、了解初中生最喜爱的电视节目 |
| B、了解某班学生数学期末考试的成绩 |
| C、估计某水库中每条鱼的平均重量 |
| D、了解一批灯泡的使用寿命 |
 二次函数y=ax2+bx+c的图象如图所示,则①abc;②b2-4ac;③2a+b;④a+b+c这四个式子中,值为负数的是
二次函数y=ax2+bx+c的图象如图所示,则①abc;②b2-4ac;③2a+b;④a+b+c这四个式子中,值为负数的是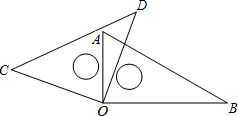 将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为
将一副三角板如图放置,若∠AOD=20°,则∠BOC的大小为