题目内容
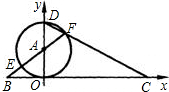 如图,直线y=-
如图,直线y=-| 1 | 2 |
(1)设F(a,b),求以a,b为根的一元二次方程;
(2)求BE的长.
分析:(1)作辅助线FO和FH,根据直径所对的圆周角是90度,构造出直角三角形OFC,利用勾股定理求出a,b的值;
(2)利用相似三角形的性质,根据相似比来求.
(2)利用相似三角形的性质,根据相似比来求.
解答: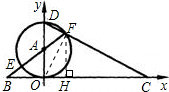 解:(1)过F作EH⊥BC,H为垂足,连接OF,由直线方程得,OD=4,OC=8,CD=4
解:(1)过F作EH⊥BC,H为垂足,连接OF,由直线方程得,OD=4,OC=8,CD=4
,
∵∠OFD为直径OD所对圆周角,
∴OF⊥DC,OF=
=
,
在Rt△OFC中,FC=
=
,FH=
=
,OH=
=
,
∴a=
,b=
,
∴所求方程为x2-
x+
=0;
(2)∵在Rt△BAO和Rt△BFH中,∠B为公共角,
∴Rt△BAO∽Rt△BFH,
∴
=
,
=
=
,
∴BE=
.
 解:(1)过F作EH⊥BC,H为垂足,连接OF,由直线方程得,OD=4,OC=8,CD=4
解:(1)过F作EH⊥BC,H为垂足,连接OF,由直线方程得,OD=4,OC=8,CD=4| 5 |
∵∠OFD为直径OD所对圆周角,
∴OF⊥DC,OF=
| OD•OC |
| DC |
| 8 |
| 5 |
| 5 |
在Rt△OFC中,FC=
| OC2-OF2 |
| 16 |
| 5 |
| 5 |
| OF×FC |
| OC |
| 16 |
| 5 |
| OF2-FH2 |
| 8 |
| 5 |
∴a=
| 8 |
| 5 |
| 16 |
| 5 |
∴所求方程为x2-
| 24 |
| 5 |
| 128 |
| 25 |
(2)∵在Rt△BAO和Rt△BFH中,∠B为公共角,
∴Rt△BAO∽Rt△BFH,
∴
| BA |
| BF |
| AO |
| FH |
| BE+2 |
| BE+4 |
| 2 | ||
|
| 5 |
| 8 |
∴BE=
| 4 |
| 3 |
点评:此题结合了圆的相关定理和勾股定理以及根据方程的根构造一元二次方程,综合性较强且难度适中,是一道好题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )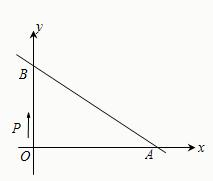 点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止. 如图,直线
如图,直线 如图,直线
如图,直线