题目内容
2.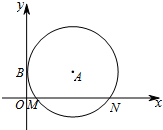 如图,在平面直角坐标系xOy中,⊙A与y轴相切于点B(0,$\frac{3}{2}$),与x轴相交于M、N两点.如果点M的坐标为($\frac{1}{2}$,0),求⊙A的半径及点N的坐标.
如图,在平面直角坐标系xOy中,⊙A与y轴相切于点B(0,$\frac{3}{2}$),与x轴相交于M、N两点.如果点M的坐标为($\frac{1}{2}$,0),求⊙A的半径及点N的坐标.
分析 连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,由切线的性质得出AB⊥y轴,由题意得出AB=AM=R,CM=R-$\frac{1}{2}$,AC=$\frac{3}{2}$,MN=2CM,由勾股定理得出方程,解方程求出R,得出CM,得出ON的长即可.
解答 解: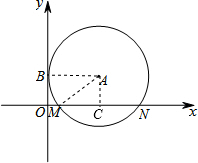 连接AB、AM、过A作AC⊥MN于C,如图所示:
连接AB、AM、过A作AC⊥MN于C,如图所示:
设⊙A的半径是R,
∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点B(0,$\frac{3}{2}$),与x轴相交于M、N两点,点M的坐标为($\frac{1}{2}$,0),
∴AB=AM=R,CM=R-$\frac{1}{2}$,AC=$\frac{3}{2}$,MN=2CM,
由勾股定理得:R2=(R-$\frac{1}{2}$)2+($\frac{3}{2}$)2,
解得:R=2.5,即⊙A的半径为2.5;
∴CM=CN=2.5-$\frac{1}{2}$=2,
∴ON=$\frac{1}{2}$+2+2=4$\frac{1}{2}$,
即N的坐标是(4$\frac{1}{2}$,0).
点评 本题考查了切线的性质、坐标与图形性质、勾股定理;熟练掌握切线的性质,由勾股定理得出方程求出半径是解决问题的关键.

练习册系列答案
相关题目
14.一元二次方程(x-1)2=0的解为( )
| A. | x=1 | B. | x=0 | C. | x=-1 | D. | x=±1 |

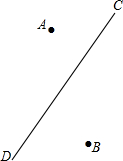 一辆货车在公路(直线CD)上由点C向点D方向行驶,村庄A、B分别位于道路CD的两侧,司机师傅要在公路上选择一个货物的下货点.
一辆货车在公路(直线CD)上由点C向点D方向行驶,村庄A、B分别位于道路CD的两侧,司机师傅要在公路上选择一个货物的下货点.