题目内容
9. 如图,直线a,b相交于点O,点P是平面上的一点,以OP为直径的⊙M交直线a、b分别为A、B.
如图,直线a,b相交于点O,点P是平面上的一点,以OP为直径的⊙M交直线a、b分别为A、B.(1)求证:∠AOP与∠ABO互余;
(2)若OA=5,AB=6,∠ABO=30°,求点M到弦AB的距离.
分析 (1)连接AP,根据圆周角定理得到∠OAP=90°,根据圆周角定理证明即可;
(2)根据直角三角形的性质得到OP=2OA=10,求出半径,根据勾股定理计算即可.
解答 (1)证明:连接AP,
∵OP为⊙M的直径,
∴∠OAP=90°,
∴∠AOP+∠P=90°,
∵∠P=∠ABO,
∴∠AOP+∠ABO=90°,
即∠AOP与∠ABO互余;
(2)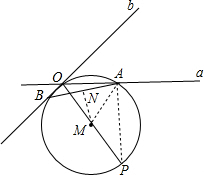 连接MA,作MN⊥AB于N,
连接MA,作MN⊥AB于N,
∠P=∠ABO=30°,
∴OP=2OA=10,
∴MA=5,
∵MN⊥AB,
∴AN=$\frac{1}{2}$AB=3,
由勾股定理得,MN=$\sqrt{M{A}^{2}-A{N}^{2}}$=4.
点评 本题考查的是圆周角定理的应用,掌握直径所对的圆周角是直角、同弧所对的圆周角相等是解题的关键.

练习册系列答案
相关题目
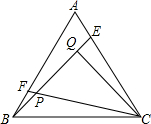 如图所示,点E、F分别是正△ABC的边AC、AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=7.
如图所示,点E、F分别是正△ABC的边AC、AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=7.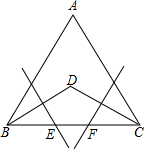 如图,△ABC是正三角形,∠B和∠C的平分线相交于D,BD,CD的垂直平分线分别交BC于E,F.求证:BE=CF.
如图,△ABC是正三角形,∠B和∠C的平分线相交于D,BD,CD的垂直平分线分别交BC于E,F.求证:BE=CF. 已知:如图D、E分别在AB、AC 上,且AB=AC,添加一个条件,使△AEB≌△ADC,有几种添法?写出来.并选择其中一种写出证明过程.
已知:如图D、E分别在AB、AC 上,且AB=AC,添加一个条件,使△AEB≌△ADC,有几种添法?写出来.并选择其中一种写出证明过程.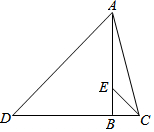 如图,已知AB⊥CD,△ABD和△BCE都是等腰直角三角形,CD=17,BE=5,则AC的长为多少?
如图,已知AB⊥CD,△ABD和△BCE都是等腰直角三角形,CD=17,BE=5,则AC的长为多少?