题目内容
设P是等边△ABC内任意一点,从点P作三边的垂线PD、PE、PF,点D、E、F是垂足,则
等于( )
| PD+PE+PF |
| AB+BC+CA |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据等边△ABC面积的计算即可求得PD+PE+PF=等边△ABC的高,根据等边△ABC的高线长和边长的比值即可解题.
解答: 解:设等边三角形的高为h,则h=
解:设等边三角形的高为h,则h=
AB,
△ABC的面积等于△PAB、△PBC、△PAC的面积之和,
故
(AB•PD+BC•PE+AC•PE)=
•BC•h,
即PD+PE+PF=h,
∴
=
=
=
.
故选B.
 解:设等边三角形的高为h,则h=
解:设等边三角形的高为h,则h=
| ||
| 2 |
△ABC的面积等于△PAB、△PBC、△PAC的面积之和,
故
| 1 |
| 2 |
| 1 |
| 2 |
即PD+PE+PF=h,
∴
| PD+PE+PF |
| AB+BC+CA |
| h |
| AB+BC+AC |
| ||||
| 3 AB |
| ||
| 6 |
故选B.
点评:本题考查了等边三角形面积的计算,等边三角形各边长相等的性质,等边三角形高线长和边长的比值,本题中求证PD+PE+PF=h是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 3、如图,设P是等边△ABC内的一点,PA=3,PB=4,PC=5,则∠APB的度数是
3、如图,设P是等边△ABC内的一点,PA=3,PB=4,PC=5,则∠APB的度数是 22、如图.设P是等边△ABC内的一点,且PA:PB:PC=3:4:5,求∠APB的度数.
22、如图.设P是等边△ABC内的一点,且PA:PB:PC=3:4:5,求∠APB的度数.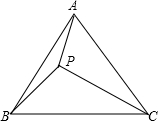 如图.设P是等边△ABC内的一点,且PA:PB:PC=3:4:5,求∠APB的度数.
如图.设P是等边△ABC内的一点,且PA:PB:PC=3:4:5,求∠APB的度数.