题目内容
方程x2+px+q=0有一根是零,另一根非零,则p、q的值是( )
| A、p=0 q=0 |
| B、p=0 q≠0 |
| C、p≠0 q=0 |
| D、pq=0 |
考点:根与系数的关系
专题:
分析:根据根与系数的关系和已知条件可得x1•x2=q=0,x1+x2=-p≠0,从而得出答案.
解答:解:∵方程x2+px+q=0有一根是零,
∴x1•x2=q=0,
∵方程x2+px+q=0另一根非零,
∴x1+x2=-p≠0,
∴p≠0,
故选:C.
∴x1•x2=q=0,
∵方程x2+px+q=0另一根非零,
∴x1+x2=-p≠0,
∴p≠0,
故选:C.
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法,关键掌握x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
如果解分式方程
-
=1出现了增根,那么增根是( )
| x+2 |
| x-3 |
| 1 |
| x+4 |
| A、-2 | B、3 | C、3或-4 | D、-4 |
 写出数字转换机示意图的转换步骤并填表.
写出数字转换机示意图的转换步骤并填表.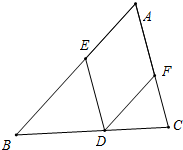 菱形AEDF内接于△ABC,且AB=21cm,AC=15cm,BC=18cm,求BD,CD及菱形的边长.
菱形AEDF内接于△ABC,且AB=21cm,AC=15cm,BC=18cm,求BD,CD及菱形的边长.