题目内容
已知△ABC的三边AC=6,BC=8,AB=10,求△ABC的内切圆的面积.
考点:三角形的内切圆与内心,勾股定理的逆定理
专题:
分析:首先判断出△ABC的形状,然后借助三角形面积的不变形,求出内切圆的半径,问题即可解决.
解答:解:∵62+82=102,
∴△ABC为直角三角形,且∠C=90°;
∴S△ABC=
AC•BC=
×6×8=24;
设△ABC内切圆的圆心为O,半径为r,
则圆心O到三边的距离均为r;
连接OA、OB、OC;
则S△ABC=S△AOC+S△BOC+S△AOB,
即24=
(6+8+10)r,
解得r=2,
∴△ABC的内切圆的面积
=πr2=4π,
即△ABC的内切圆的面积为4π.
∴△ABC为直角三角形,且∠C=90°;
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
设△ABC内切圆的圆心为O,半径为r,
则圆心O到三边的距离均为r;
连接OA、OB、OC;
则S△ABC=S△AOC+S△BOC+S△AOB,
即24=
| 1 |
| 2 |
解得r=2,
∴△ABC的内切圆的面积
=πr2=4π,
即△ABC的内切圆的面积为4π.
点评:该题在考查三角形的内切圆及其圆心性质的同时,还渗透了对勾股定理、三角形的面积公式等知识点的考查;灵活解题是关键.

练习册系列答案
相关题目
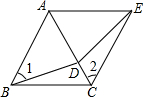 已知:如图所示,D在等边△ABC的边AC上,∠ACE=∠ABD,CE=BD.试说明:
已知:如图所示,D在等边△ABC的边AC上,∠ACE=∠ABD,CE=BD.试说明: 已知,如图,点B,C,E在一条直线上,AB⊥BE,DE⊥BE,且AB=CE,BC=DE.
已知,如图,点B,C,E在一条直线上,AB⊥BE,DE⊥BE,且AB=CE,BC=DE. 如图,点P是等边△ABC内的一点,分别连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接PQ、QC.
如图,点P是等边△ABC内的一点,分别连接PA、PB、PC,以BP为边作∠PBQ=60°,且BQ=BP,连接PQ、QC. 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.求证:∠ACM=∠ABC.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.求证:∠ACM=∠ABC.