Question

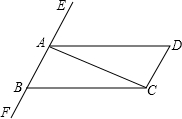如图，要使AD∥BC，则需添加一个条件，请写出三种情况，并写出简单的推理过程和理由
解：
（1）由

∠EAD=∠ABC

（填条件）
得AD∥BC（

同位角相等，两直线平行

 ）
（2）

由∠DAC=∠ACB，
得AD∥BC（内错角相等，两直线平行）

；
（3）

由∠DAB+∠ABC=180°，
得AD∥BC（同旁内角互补，两直线平行）．

．

Answer 1

分析：利用平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行求解即可求得答案，注意此题答案不唯一．

解答：解：（1）由∠EAD=∠ABC，
得AD∥BC（同位角相等，两直线平行）；

（2）由∠DAC=∠ACB，
得AD∥BC（内错角相等，两直线平行）；

（3）由∠DAB+∠ABC=180°，
得AD∥BC（同旁内角互补，两直线平行）．
故答案为：（1）∠EAD=∠ABC，同位角相等，两直线平行；
（2）由∠DAC=∠ACB，
得AD∥BC（内错角相等，两直线平行）；
（3）由∠DAB+∠ABC=180°，
得AD∥BC（同旁内角互补，两直线平行）．

点评：此题考查了平行线的判定．此题比较简单，注意掌握数形结合思想的应用．