题目内容
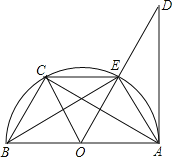
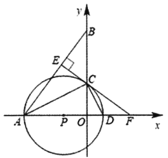
【题目】如图所示，在△DEF中，EF＝10，DF＝6，DE＝8，以EF的中点O为圆心，作半圆与DE相切，点A、B分别是半圆和边DF上的动点，连接AB，则AB的最大值与最小值的和是（ ）
A.6B.2
+1C.
D.9
【答案】D
【解析】
先确定AB的最大值与最小值，作辅助线，构建矩形OCDB，则此时AB最小，图中FN就是AB的最大值，根据勾股定理和中位线定理可得结论．
如图，设⊙O与DE相切于点C，连接OC，作
于点B，交⊙O于点A
由点与圆的位置关系得：图中AB最小，最小值为
；当点A在点N处，点B在点F处时，AB最大，最大值为FN
由勾股定理得：
由圆的切线的性质得：
，即圆的半径为3
则AB的最小值为
，AB的最大值为
因此，AB的最大值与最小值的和是
故选：D．
练习册系列答案
相关题目
