题目内容
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上一点,
轴上一点,![]() 经过点
经过点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 的延长线交
的延长线交![]() 轴于点
轴于点![]() ,
,
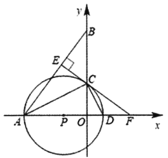
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求![]() 的半径.
的半径.
【答案】(1)证明见解析;(2)5.
【解析】
(1)连接CP,根据等腰三角形的性质得到∠PAC=∠PCA,由角平分线的定义得到∠PAC=∠EAC,等量代换得到∠PCA=∠EAC,推出PC∥AE,于是得到结论;
(2)连接PC,根据角平分线的定义得到∠BAC=∠OAC,根据等腰三角形的性质得到∠PCA=∠PAC,等量代换得到∠BAC=∠ACP,推出PC∥AB,根据相似三角形的性质即可得到结论.
(1) 证明:连接![]() ,
,

∵![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() 是
是![]() 的切线.
的切线.
(2)连接![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴ ,
,
∴![]() ,
,
∴![]() 的半径为5
的半径为5

练习册系列答案
相关题目
【题目】某水果公司以2.2元/千克的成本价购进![]() 苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果损坏的频率 | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为______精确到0.1),据此,若公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为______元/千克.