题目内容
12. 如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为(225+25$\sqrt{2}$)π.
如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为(225+25$\sqrt{2}$)π.
分析 根据给出的几何体的三视图可知几何体是由圆柱体和圆锥体构成,从而根据三视图的特点得知高和底面直径,代入表面积公式计算即可.
解答 解:由三视图可知,几何体是由圆柱体和圆锥体构成,
故该几何体的表面积为:20×10π+π×52+$\frac{1}{2}$×10π×$\sqrt{{5}^{2}+{5}^{2}}$=(225+25$\sqrt{2}$)π
故答案是:(225+25$\sqrt{2}$)π.
点评 本题考查了由三视图判断几何体,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.

练习册系列答案
相关题目
20. 如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )
如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )
 如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )
如图,已知正方形ABCD,点E是BC边的中点,DE与AC相交于点F,连接BF,下列结论:①S△ABF=S△ADF;②S△CDF=4S△CEF;③S△ADF=2S△CEF;④S△ADF=2S△CDF,其中正确的是( )| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
7.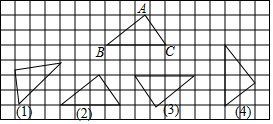 图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
 图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )
图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
3.$\frac{4}{9}$的分子加上12,要使原分数大小不变,分母应加上…( )
| A. | 12 | B. | 27 | C. | 36 | D. | 45 |
7.下列实数是无理数的是( )
| A. | 1 | B. | 0 | C. | -$\frac{1}{2}$ | D. | $\sqrt{3}$ |
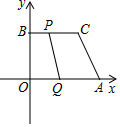 如图,在平面直角坐标系中,点A、B的坐标分别为(a,0)、(0,b),其中a、b满足|a+b-34|+|-a+b+18|=0,将点B向右平移24个单位得到点C.
如图,在平面直角坐标系中,点A、B的坐标分别为(a,0)、(0,b),其中a、b满足|a+b-34|+|-a+b+18|=0,将点B向右平移24个单位得到点C.