��Ŀ����
19��ͨ��������롢������չ�о�������Ŀ���ɴﵽ��һ��֪һ���Ŀ�ģ�������һ���������벹��������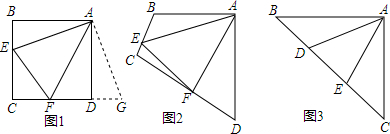
ԭ�⣺��ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45�㣬����EF����֤��EF=BE+DF��
��1��˼·����
��AB=AD����ѡ�ABE�Ƶ�A��ʱ����ת90������ADG����ʹAB��AD�غϣ�
�ߡ�ADG=��B=90�㣬���FDG=��ADG+��ADC=180�㣬���F��D��G���ߣ�
����SAS����֤��AFG�ա�AFE���Ӷ���EF=BE+DF��
��2���������
��ͼ2���ı���ABCD�У�AB=AD����BAD=90���E��F�ֱ��ڱ�BC��CD�ϣ���EAF=45�㣮����B����D������ֱ�ǣ�������B���D���������ϵ��B+��D=180��ʱ������EF=BE+DF�������֤����
��3��������չ
��ͼ3���ڡ�ABC�У���BAC=90�㣬AB=AC����D��E���ڱ�BC�ϣ��ҡ�DAE=45�㣬����BD��DE��ECӦ����ĵ�����ϵ����д���������̣�
���� ��1���ѡ�ABE�Ƶ�A��ʱ����ת90������ADG����ʹAB��AD�غϣ���֤����AFG�ա�AFE�����õ�EF=FG�����ɵ�EF=BE+DF��
��2����B+��D=180��ʱ��EF=BE+DF���루1����֤����ͬ��
��3�����ݡ�AEC�Ƶ�A˳ʱ����ת90��õ���ABE�䣬������ת�����ʣ���֪��AEC�ա�ABE��õ�BE��=EC��AE��=AE����C=��ABE�䣬��EAC=��E��AB������Rt��ABC�еģ�AB=AC�õ���E��BD=90�㣬����E��B2+BD2=E��D2��֤��AE��D�ա�AED������DE=DE��õ�DE2=BD2+EC2��
���  �⣺��1����ͼ1����AB=AD��
�⣺��1����ͼ1����AB=AD��
��ѡ�ABE�Ƶ�A��ʱ����ת90������ADG����ʹAB��AD�غϣ�
���BAE=��DAG��
�ߡ�BAD=90�㣬��EAF=45�㣬
���BAE+��DAF=45�㣬
���EAF=��FAG��
�ߡ�ADC=��B=90�㣬
���FDG=180�㣬��F��D��G���ߣ�
�ڡ�AFE�͡�AFG��
$\left\{\begin{array}{l}{AE=AG}\\{��EAF=��FAG}\\{AF=AF}\end{array}\right.$��
���AFE�ա�AFG��SAS����
��EF=FG��
����EF=BE+DF��
�ʴ�Ϊ��SAS����AFE��
��2����B+��D=180��ʱ��EF=BE+DF��
��ͼ2����AB=AD��
��ѡ�ABE�Ƶ�A��ʱ����ת90������ADG����ʹAB��AD�غϣ�
���BAE=��DAG��
�ߡ�BAD=90�㣬��EAF=45�㣬
���BAE+��DAF=45�㣬
���EAF=��FAG��
�ߡ�ADC+��B=180�㣬
���FDG=180�㣬��F��D��G���ߣ�
�ڡ�AFE�͡�AFG��
$\left\{\begin{array}{l}{AE=AG}\\{��EAF=��FAG}\\{AF=AF}\end{array}\right.$��
���AFE�ա�AFG��SAS����
��EF=FG��
����EF=BE+DF��
�ʴ�Ϊ����B+��D=180�㣻
��3�����룺DE2=BD2+EC2��
֤������ͼ3������DE�䣬���ݡ�AEC�Ƶ�A˳ʱ����ת90��õ���ABE�䣬
���AEC�ա�ABE�䣬
��BE��=EC��AE��=AE��
��C=��ABE�䣬��EAC=��E��AB��
��Rt��ABC��
��AB=AC��
���ABC=��ACB=45�㣬
���ABC+��ABE��=90�㣬
����E��BD=90�㣬
��E��B2+BD2=E��D2��
�֡ߡ�DAE=45�㣬
���BAD+��EAC=45�㣬
���E��AB+��BAD=45�㣬
����E��AD=45�㣬
�ڡ�AE��D�͡�AED�У�
$\left\{\begin{array}{l}{AE��=AE}\\{��E��AD=��DAE}\\{AD=AD}\end{array}\right.$��
���AE��D�ա�AED��SAS����
��DE=DE�䣬
��DE2=BD2+EC2��
���� ������Ҫ�����˼��α任���ؼ�����ȷ����ͼ�Σ�֤����AFG�ա�AEF��������һ���ۺ��⣬�ѶȽϴ���Ŀ���������˼·��Ϊ����������˽Ϻõ��̵森

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�| ��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ���ߴ� |
| -4 | +7 | -9 | +8 | +6 | -5 | -2 |
��2����ά��С�鷵�ص�A��ʱ����ÿkm����0.3�����ʹ����Ͷ�������
| A�� | 4a6 | B�� | 4a5 | C�� | 2a6 | D�� | 2a5 |
 ��֪���κ���y=ax2+bx+c�IJ���ͼ����ͼ��ʾ����Գ���Ϊֱ��x=-1��������x���һ������ΪA��2��0��������ͼ���֪�����Ա���x��ȡֵ��Χ��x��2��x��-4ʱ������ֵy��0��
��֪���κ���y=ax2+bx+c�IJ���ͼ����ͼ��ʾ����Գ���Ϊֱ��x=-1��������x���һ������ΪA��2��0��������ͼ���֪�����Ա���x��ȡֵ��Χ��x��2��x��-4ʱ������ֵy��0��
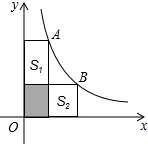 ��ͼ��A��B������˫����y=$\frac{6}{x}$�ϣ�����A��B����ֱ��������������߶Σ���֪S��Ӱ=1����S1+S2=10��
��ͼ��A��B������˫����y=$\frac{6}{x}$�ϣ�����A��B����ֱ��������������߶Σ���֪S��Ӱ=1����S1+S2=10��