题目内容
15．已知二次函数y=3x2+c与正比例函数y=4x的图象只有一个交点，则c的值为$\frac{4}{3}$．分析 将一次函数解析式代入到二次函数解析式中，得出关于x的一元二次方程，由两函数图象只有一个交点可得知该方程有两个相同的实数根，结合根的判别式即可得出关于c的一元一次方程，解方程即可得出结论．
解答 解：将正比例函数y=4x代入到二次函数y=3x2+c中，
得：4x=3x2+c，即3x2-4x+c=0．
∵两函数图象只有一个交点，
∴方程3x2-4x+c=0有两个相等的实数根，
∴△=（-4）2-4×3c=0，
解得：c=$\frac{4}{3}$．
故答案为：$\frac{4}{3}$．
点评 本题考查了根的判别式，解题的关键是根据函数图象的交点个数得出方程根的个数．本题属于基础题，难度不大，解决该题型题目时，根据函数交点的个数结合根的判别式得出不等式（或方程）是关键．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
6．
长方体的主视图与左视图如图所示（单位：cm），则其俯视图的面积是（ ）
长方体的主视图与左视图如图所示（单位：cm），则其俯视图的面积是（ ）| A． | 4cm2 | B． | 6cm2 | C． | 8cm2 | D． | 12cm2 |
3．从0，π，$\frac{1}{3}$，$\frac{{\sqrt{2}}}{2}$这四个数中随机取出一个数，取出的数是无理数的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
由4个相同小立方体搭成的几何体如图所示，则它的俯视图是（ ）
20．2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（ ）
| A． | b=a（1+8.9%+9.5%） | B． | b=a（1+8.9%×9.5%） | ||
| C． | b=a（1+8.9%）（1+9.5%） | D． | b=a（1+8.9%）2（1+9.5%） |
7．
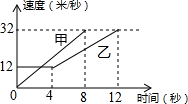如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（ ）
如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（ ）| A． | 乙前4秒行驶的路程为48米 | |
| B． | 在0到8秒内甲的速度每秒增加4米/秒 | |
| C． | 两车到第3秒时行驶的路程相等 | |
| D． | 在4至8秒内甲的速度都大于乙的速度 |
4．若x2-3y-5=0，则6y-2x2-6的值为（ ）
| A． | 4 | B． | -4 | C． | 16 | D． | -16 |
如图所示，四边形ABCD的对角线相交于点O，若AB∥CD，请添加一个条件AD∥BC（写一个即可），使四边形ABCD是平行四边形．