��Ŀ����
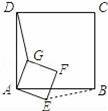
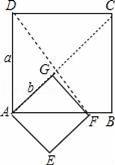
��ͼ��������ABCD��������AEFG��һ��������A����G��E�ֱ����߶�AD��AB�ϣ�
��1������DF��BF������������AEFG�Ƶ�A��˳ʱ�뷽����ת���ж����⡰����ת�Ĺ����У��߶�DF��BF�ij�ʼ����ȡ��Ƿ���ȷ������ȷ����֤����������ȷ�������˵����
��2������������AEFG�Ƶ�A��˳ʱ�뷽����ת������DG������ת�����У����ܷ��ҵ�һ���߶εij����߶�DG�ij�ʼ����ȣ�����ͼΪ��˵�����ɣ�


��
�����㡿��ת�����ʣ�ȫ�������ε��ж������ʣ������ε����ʣ�
��ר�⡿����ͼ�����⣻�ۺ��⣮
����������1����Ȼ����A��F��B��ͬһֱ����ʱ��DF��BF��
��2��ע��ʹ�����������εıߺ�90��Ľǣ����жϳ���DAG�ա�BAE����ôDG=BE��
����𡿽⣺��1������ȷ��
����������GAEF�Ƶ�A˳ʱ����ת45�㣬��ʱ��F�����߶�AB��AB���ӳ����ϣ�����������GAEF�Ƶ�A˳ʱ����ת��ʹ�õ�F�����߶�AB��AB���ӳ����ϣ�����ͼ��
��AD=a��AG=b��
��DF=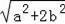
 ��a��
��a��
BF=|AB��AF|=|a��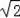
 b|��a��
b|��a��
��DF��BF������ʱDF��BF��
��2������BE���ɵá�ADG�ա�ABE��
��DG=BE����ͼ��
���ı���ABCD�������Σ�
��AD=AB��
���ı���GAEF�������Σ�
��AG=AE��
�֡ߡ�DAG+��GAB=90�㣬��BAE+��GAB=90�㣬
���DAG=��BAE��
���DAG�ա�BAE��
��DG=BE��


��������ע���������λ��ʱ���õ��Ĺ�ϵ���жϱ���ȣ�ͨ��Ҫ��ȫ�������Σ�
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�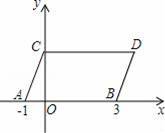


 |+2��
|+2��
 ��
��