Question

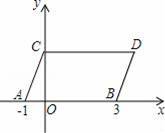
如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A、B 的对应点C，D，连接AC，BD，CD．

（1）求点C，D的坐标及四边形ABDC的面积S_{四边形ABDC}；

（2）在y轴上是否存在一点P，连接PA，PB，使S_△PAB=S_{四边形ABDC}？若存在这样一点，求出点P的坐标；若不存在，试说明理由．

Answer 1

【考点】坐标与图形性质；三角形的面积；坐标与图形变化-平移．

【分析】（1）根据向右平移横坐标加，向上平移纵坐标加写出点C、D的坐标即可，再根据平行四边形的面积公式列式计算即可得解；

（2）假设y轴上存在P（0，b）点，使S_△PAB=S_{四边形ABDC}，列方程，解得b．

【解答】解：（1）C（0，2），D（4，2），

四边形ABCD的面积=（3+1）×2=8；

（2）假设y轴上存在P（0，b）点，则S_△PAB=S_{四边形ABDC}

∴|AB|•|b|=8，

∴b=±4，

∴P（0，4）或P（0，﹣4）．

【点评】本题考查平移有关知识．平移的基本性质是：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．