题目内容
3.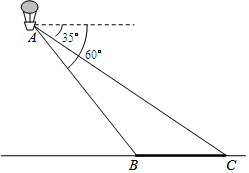 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.
如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.(结果保留整数,参考数据:sin35°≈$\frac{7}{12}$,cos35°≈$\frac{5}{6}$,tan35°≈$\frac{7}{10}$,$\sqrt{3}$≈1.7)
分析 作AD⊥CB交CB所在直线于点D,利用锐角三角函数的定义求出CD及BD的长,利用BC=CD-BD即可得出结论.
解答  解:作AD⊥CB交CB所在直线于点D,由题知,
解:作AD⊥CB交CB所在直线于点D,由题知,
∠ACD=35°,∠ABD=60°,
∵在Rt△ACD中,∠ACD=35°,tan35°=$\frac{AD}{CD}$≈$\frac{7}{10}$,
∴CD=$\frac{10}{7}$AD.
∵在Rt△ABD中,∠ABD=60°,tan60°=$\frac{AD}{BD}$=$\sqrt{3}$≈1.7,
∴BD=$\frac{10}{17}$AD,
∴BC=CD-BD=$\frac{10}{7}$AD-$\frac{10}{17}$AD,
∴$\frac{10}{7}$AD-$\frac{10}{17}$AD=100,解得AD=119m.
答:热气球离地面的高119m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
20. 如图,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点B1的坐标为( )
如图,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点B1的坐标为( )
 如图,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点B1的坐标为( )
如图,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点B1的坐标为( )| A. | (-4,2) | B. | (-2,4) | C. | (4,-2) | D. | (2,-4) |
11.有甲、乙、丙三种糖果混合而成的什锦糖100千克,其中各种糖果的单价和千克数如表所示,商家用加权平均数来确定什锦糖的单价.
(1)求该什锦糖的单价.
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 20 | 25 | 30 |
| 千克数 | 40 | 40 | 20 |
(2)为了使什锦糖的单价每千克至少降低2元,商家计划在什锦糖中加入甲、丙两种糖果共100千克,问其中最多可加入丙种糖果多少千克?
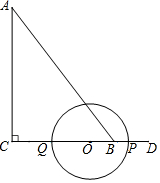 如图,在△ABC中,∠ACB=90°,AC=8,CB=6,点D在线段CB的延长线上,且BD=2,点P从点D出发沿着DC向终点C以每秒1个单位的速度运动,同时点Q从点C出发沿着折线C-B-A往终点A以每秒2个单位的速度运动.以PQ为直径构造⊙O,设运动的时间为t(t≥0)秒.
如图,在△ABC中,∠ACB=90°,AC=8,CB=6,点D在线段CB的延长线上,且BD=2,点P从点D出发沿着DC向终点C以每秒1个单位的速度运动,同时点Q从点C出发沿着折线C-B-A往终点A以每秒2个单位的速度运动.以PQ为直径构造⊙O,设运动的时间为t(t≥0)秒.