题目内容
16．（1）计算：（4$\sqrt{2}$-3$\sqrt{6}$）÷2$\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$（2）解方程：5x2-4x-1=0．
分析 （1）先进行二次根式的除法运算，然后合并即可；
（2）利用因式分解法解方程．
解答 解：（1）原式=2-$\frac{3\sqrt{3}}{2}$+$\frac{3\sqrt{3}}{2}$
=2；
（2）（5x+1）（x-1）=0，
5x+1=0或x-1=0，
所以x1=-$\frac{1}{5}$，x2=1．
点评 本题考查了二次根式的计算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．也考查了因式分解法解一元二次方程．
练习册系列答案
相关题目
6．
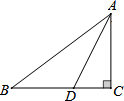如图，在Rt△ABC中，AD平分∠BAC，AC=BC，∠C=Rt∠，那么$\frac{AC}{DC}$的值为（ ）
如图，在Rt△ABC中，AD平分∠BAC，AC=BC，∠C=Rt∠，那么$\frac{AC}{DC}$的值为（ ）| A． | （$\sqrt{2}$-1）：1 | B． | （$\sqrt{2}$+1）：1 | C． | $\sqrt{2}$：1 | D． | 2：1 |
4．某校春季运动会比赛中，八年级（1）班、（5）班的竞技实力相当，（1）班与（5）班得分比为6：5，（1）班得分比（5）班得分的2倍少40分，若设（1）班得x分，（5）班得y分，根据题意所列的方程组应为（ ）
| A． | $\left\{\begin{array}{l}{5x=6y}\\{x=2y-40}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{5x=6y}\\{x=2y+40}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{6x=5y}\\{x=2y+40}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{6x=5y}\\{x=2y-40}\end{array}\right.$ |