题目内容
某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A. 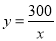 (x>0) B.
(x>0) B. 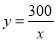 (x≥0) C. y=300x(x≥0) D. y=300x(x>0)
(x≥0) C. y=300x(x≥0) D. y=300x(x>0)
练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
题目内容
某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A. 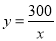 (x>0) B.
(x>0) B. 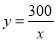 (x≥0) C. y=300x(x≥0) D. y=300x(x>0)
(x≥0) C. y=300x(x≥0) D. y=300x(x>0)
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案