题目内容
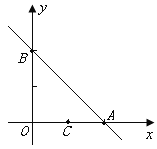
如图,一次函数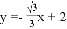 与坐标轴分别交于A,B两点,抛物线
与坐标轴分别交于A,B两点,抛物线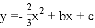 经过点A,B,点P从点B出发,以每秒2个单位长度的速度沿射线BA运动,点Q从点A出发,以每秒1个单位长度的速度沿射线AO运动,两点同时出发,运动时间为t秒.
经过点A,B,点P从点B出发,以每秒2个单位长度的速度沿射线BA运动,点Q从点A出发,以每秒1个单位长度的速度沿射线AO运动,两点同时出发,运动时间为t秒.
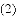
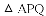
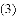
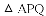
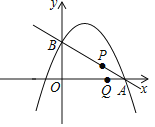
练习册系列答案
相关题目
为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
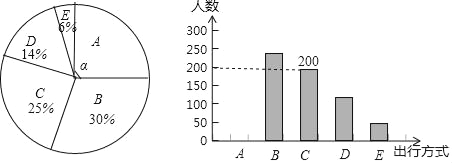
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.


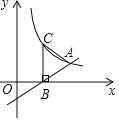
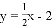 与x轴交于点B,与双曲线
与x轴交于点B,与双曲线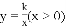 交于点A,过点B作x轴的垂线,与双曲线
交于点A,过点B作x轴的垂线,与双曲线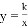 交于点
交于点
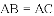
 ,当宇宙中一块陨石落在地球上,则落在陆地上的概率是
,当宇宙中一块陨石落在地球上,则落在陆地上的概率是

 B.
B.  C.
C.  D.
D. 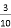


 B.
B. 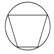 C.
C. 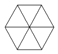 D.
D. 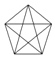
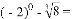 ______.
______.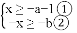 在同一条数轴上表示不等式①②的解集如图,则b-a的值为____.
在同一条数轴上表示不等式①②的解集如图,则b-a的值为____.
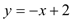 与
与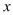 轴、
轴、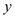 轴交点分别为
轴交点分别为 、
、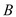 ,另一直线
,另一直线
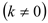 经过
经过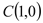 ,且把
,且把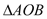 分成两部分.
分成两部分.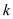 和
和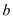 的值.
的值.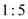 ,求
,求