题目内容
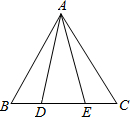 如图,AD=AE,∠ADB=∠AEC,BD=CE,则△ABD≌△________,△ABE≌△________.
如图,AD=AE,∠ADB=∠AEC,BD=CE,则△ABD≌△________,△ABE≌△________.
ACE ACD
分析:利用“边角边”证明△ABD和△ACE全等;
先根据等角的补角相等求出∠AEB=∠ADC,再求出BE=CD,然后利用“边角边”证明△ABE和△ACD全等.
解答:在△ABD和△ACE中,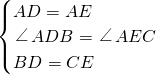 ,
,
∴△ABD≌△ACE(SAS);
∵∠ADB=∠AEC,
∴180°-∠ADB=180°-∠AEC,
即∠AEB=∠ADC,
∵BD=CE,
∴BD+DE=CE+DE,
即BE=CD,
在△ABE和△ACD中,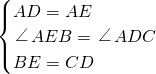 ,
,
∴△ABE≌△ACD(SAS).
故答案为:ACE;ACD.
点评:本题考查了全等三角形的判定,主要利用了“边角边”证明两三角形全等,是基础题,结合图形确定出全等的三角形是解题的关键.
分析:利用“边角边”证明△ABD和△ACE全等;
先根据等角的补角相等求出∠AEB=∠ADC,再求出BE=CD,然后利用“边角边”证明△ABE和△ACD全等.
解答:在△ABD和△ACE中,
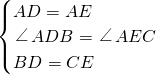 ,
,∴△ABD≌△ACE(SAS);
∵∠ADB=∠AEC,
∴180°-∠ADB=180°-∠AEC,
即∠AEB=∠ADC,
∵BD=CE,
∴BD+DE=CE+DE,
即BE=CD,
在△ABE和△ACD中,
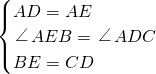 ,
,∴△ABE≌△ACD(SAS).
故答案为:ACE;ACD.
点评:本题考查了全等三角形的判定,主要利用了“边角边”证明两三角形全等,是基础题,结合图形确定出全等的三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△
2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△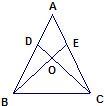 21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.
21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点. 39、已知:如图,AD=AE,AB=AC,BD、CE相交于O.
39、已知:如图,AD=AE,AB=AC,BD、CE相交于O. 23、已知:如图,AD=AE,AB=AC,DC与BE交于O点.
23、已知:如图,AD=AE,AB=AC,DC与BE交于O点. 如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=
如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=