题目内容
已知
=
=
,求:
.
| b+c-a |
| a |
| a+c-b |
| b |
| a+b-c |
| c |
| (a+b)(b+c)(c+a) |
| abc |
考点:分式的化简求值
专题:计算题
分析:设
=
=
=k,表示出b+c-a=ka①,c+a-b=kb②,a+b-c=kc③,三式相加得到a+b+c=0或k=1,即可确定出原式的值.
| b+c-a |
| a |
| a+c-b |
| b |
| a+b-c |
| c |
解答:解:设
=
=
=k,
∴b+c-a=ka①,c+a-b=kb②,a+b-c=kc③,
①+②+③得:a+b+c=k(a+b+c),即(a+b+c)(k-1)=0,
当a+b+c=0时,a+b=-c,
则原式=
=-1;
当k-1=0,即k=1时,a+b=2c,c+a=2b,b+c=2a,
则原式=
=8.
| b+c-a |
| a |
| a+c-b |
| b |
| a+b-c |
| c |
∴b+c-a=ka①,c+a-b=kb②,a+b-c=kc③,
①+②+③得:a+b+c=k(a+b+c),即(a+b+c)(k-1)=0,
当a+b+c=0时,a+b=-c,
则原式=
| -c•(-a)•(-b) |
| abc |
当k-1=0,即k=1时,a+b=2c,c+a=2b,b+c=2a,
则原式=
| 2c•2a•2b |
| abc |
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 在菱形ABCD中,∠ABC=120°,对角线AC、BD交于点O,AE平分∠CAD,分别交OD、CD于F、E两点,求∠AFO的度数.
在菱形ABCD中,∠ABC=120°,对角线AC、BD交于点O,AE平分∠CAD,分别交OD、CD于F、E两点,求∠AFO的度数.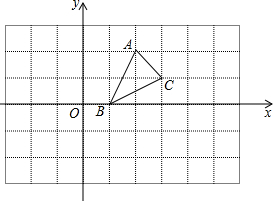 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的三个顶点的坐标分别是:A(2,2),B(1,0),C(3,1).