Question

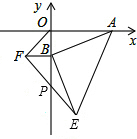如图，点A的坐标为（8，0），点B为y轴的负半轴上的一个动点，分别以OB，AB为直角边在第三、第四象限作等腰Rt△OBF，等腰Rt△ABE，连接EF交y轴于P点，当点B在y轴上移动时，PB的长度为（　　）

• A、2
• B、3
• C、4
• D、PB的长度随点B的运动而变化

Answer 1

考点：全等三角形的判定与性质,坐标与图形性质

专题：

分析：作EN⊥y轴于N，求出∠NBE=∠BAO，证△ABO≌△BEN，求出∠OBF=∠FBP=∠BNE=90°，证△BFP≌△NEP，推出BP=NP，即可得出答案．

解答：解：如图，作EN⊥y轴于N，
∵∠ENB=∠BOA=∠ABE=90°，
∴∠OBA+∠NBE=90°，∠OBA+∠OAB=90°，
∴∠NBE=∠BAO，
在△ABO和△BEN中，

∠AOB=∠BNE ∠BAO=∠NBE AB=BE

，
∴△ABO≌△BEN（AAS），
∴OB=NE=BF，
∵∠OBF=∠FBP=∠BNE=90°，
在△BFP和△NEP中，

∠FPB=∠EPN ∠FBP=∠ENP BF=NE

，
∴△BFP≌△NEP（AAS），
∴BP=NP，
又∵点A的坐标为（8，0），
∴OA=BN=8，
∴BP=NP=4，
故选：C．

点评：本题考查了全等三角形的性质和判定，坐标与图形性质等知识点的应用，主要考查学生综合运用性质进行推理和计算的能力，有一定的难度，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，全等三角形的对应角相等，对应边相等．