题目内容
20.如图1,△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.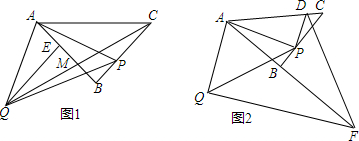
(1)求证:△PAB≌△AQE;
(2)连接CQ交AB于M,若PC=2PB,求$\frac{PC}{MB}$的值;
(3)如图2,过Q作QF⊥AQ交AB的延长线于点F,过P点作DP⊥AP交AC于D,连接DF,当点P在线段BC上运动时(不与B,C重合),式子$\frac{QF-DP}{DF}$的值会变化吗?若不变,求出该值;若变化,请说明理由.
分析 (1)根据题目中的信息可以得到AQ=AP,∠QEA与∠ABP之间的关系,∠QAE与∠APB之间的关系,从而可以解答本题;
(2)由第一问中的两个三角形全等,可以得到各边之间的关系,然后根据题目中的信息找到PC与MB的关系,从而可以解答本题;
(3)作合适的辅助线,构造直角三角形,通过三角形的全等可以找到所求问题需要的边之间的关系,从而可以解答本题.
解答 (1)证明:∵△ACB为等腰三角形,∠ABC=90°,点P在线段BC上(不与B,C重合),以AP为腰长作等腰直角△PAQ,QE⊥AB于E.
∴AP=AQ,∠ABP=∠QEA=90°,∠QAE+∠BAP=∠BAP+∠APB=90°,
∴∠QAE=∠APB,
在△PAB和△AQE中,
$\left\{\begin{array}{l}{∠ABQ=∠QEA}\\{∠QAE=∠APB}\\{AQ=PA}\end{array}\right.$,
∴△PAB≌△AQE(AAS);
(2)解:∵△PAB≌△AQE,
∴AE=PB,
∵AB=CB,
∴QE=CB.
在△QEM和△CBM中,
$\left\{\begin{array}{l}{∠QME=∠CMB}\\{∠QEM=∠CBM}\\{QE=CB}\end{array}\right.$,
∴△QEM≌△CBM(AAS),
∴ME=MB,
∵AB=CB,AE=PB,PC=2PB,
∴BE=PC,
∵PC=2PB,
∴PC=2MB,
∴$\frac{PC}{MB}=2$;
(3)式子$\frac{QF-DP}{DF}$的值不会变化.
如下图2所示:作HA⊥AC交QF于点H,
∵QA⊥AP,HA⊥AC,AP⊥PD,
∴∠QAH+∠HAP=∠HAP+∠PAD=90°,∠AQH=∠APD=90°,
∴∠QAH=∠PAD,
∵△PAQ为等腰直角三角形,
∴AQ=AP,
在△AQH和△APD中,
$\left\{\begin{array}{l}{∠AQH=∠APD}\\{AQ=AP}\\{∠QAH=∠PAD}\end{array}\right.$,
∴△AQH≌△APD(ASA),
∴AH=AD,QH=PD,
∵HA⊥AC,∠BAC=45°,
∴∠HAF=∠DAF,
在△AHF和△ADF中,
$\left\{\begin{array}{l}{AH=AD}\\{∠HAF=∠DAF}\\{AF=AF}\end{array}\right.$,
∴△AHF≌△ADF(SAS),
∴HF=DF,
∴$\frac{QF-DP}{DF}$=$\frac{QF-QH}{HF}$=$\frac{HF}{HF}$=1.
点评 本题考查全等三角形的判定与性质、等腰三角形的性质,解题的关键是利用数形结合的思想,找出所求问题需要的关系,通过三角形的全等可以得到相关的角和边之间的关系.

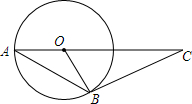 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )| A. | 65° | B. | 50° | C. | 40° | D. | 25° |
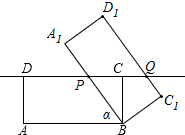 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α<8)得到矩形A1B1C1D1.这两边所在的直线分别与CD边所在的直线相交于点P,Q,当DP:DQ=1:2时,DP的长为5.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α<8)得到矩形A1B1C1D1.这两边所在的直线分别与CD边所在的直线相交于点P,Q,当DP:DQ=1:2时,DP的长为5.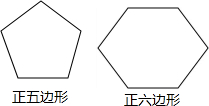 如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.
如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x. 如图,一个几何体由大小相同、棱长为1的正方体搭成,则其左视图的面积为3.
如图,一个几何体由大小相同、棱长为1的正方体搭成,则其左视图的面积为3.