题目内容
 如图,在菱形ABCD中,点E在BC上,且AE=AD,∠EAD=2∠BAE,求∠BAE的度数.
如图,在菱形ABCD中,点E在BC上,且AE=AD,∠EAD=2∠BAE,求∠BAE的度数.考点:菱形的性质
专题:
分析:根据菱形的四条边都相等可得AB=AD,从而求出AB=AE,设∠BAE=x,然后根据等腰三角形两底角相等表示出∠ABE,再根据菱形的邻角互补列出方程求解即可.
解答:解:在菱形ABCD中,AB=AD,
∵AE=AD,
∴AB=AE,
设∠BAE=x,
则∠EAD=2x,∠ABE=
(180°-x),
∵AD∥BC,
∴∠BAD+∠ABE=180°,
∴x+2x+
(180°-x)=180°,
解得x=36°,
即∠BAE=36°.
∵AE=AD,
∴AB=AE,
设∠BAE=x,
则∠EAD=2x,∠ABE=
| 1 |
| 2 |
∵AD∥BC,
∴∠BAD+∠ABE=180°,
∴x+2x+
| 1 |
| 2 |
解得x=36°,
即∠BAE=36°.
点评:本题考查了菱形的性质,等腰三角形的性质,熟记各性质并列出关于∠BAE的方程是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
某校为了解学校学生的视力情况,从全校学生中随机抽取了200个学生进行检查.则下列说法错误的是( )
| A、本次的调查方式是抽样调查 |
| B、该校每一个学生是本次调查的个体 |
| C、本次调查的样本容量是200 |
| D、被抽取的这200个学生的视力情况是本次调查的样本 |
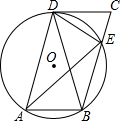 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
 如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF,若OG=2,则EF为
如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线,垂足为E、F、G,连接EF,若OG=2,则EF为