题目内容
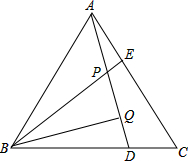 如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.(1)求证:△ABE≌△CAD;
(2)求AD的长.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据AE=CD,AB=AC,∠BAC=∠C即可求得△ABE≌△CAD;
(2)由(1)得∠AEB=∠ADC,即可求得∠BPQ=∠C,即可求得BP的长,即可解题.
(2)由(1)得∠AEB=∠ADC,即可求得∠BPQ=∠C,即可求得BP的长,即可解题.
解答:解:(1)∵在△ABE和△CAD中,
,
∴△ABE≌△CAD,(SAS)
(2)∵△ABE≌△CAD,
∴AD=BE,∠AEB=∠ADC
∵∠DAC+∠ADC+∠ACB=180°,∠DAC+∠AEB+∠APE=180°,
∴∠ACB=∠APE=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴BP=2PQ=6,
∴AD=BE=BP+PE=6+1=7.
|
∴△ABE≌△CAD,(SAS)
(2)∵△ABE≌△CAD,
∴AD=BE,∠AEB=∠ADC
∵∠DAC+∠ADC+∠ACB=180°,∠DAC+∠AEB+∠APE=180°,
∴∠ACB=∠APE=60°,
∴∠BPQ=60°,
∴∠PBQ=30°,
∴BP=2PQ=6,
∴AD=BE=BP+PE=6+1=7.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△CAD是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,⊙O为Rt△ABC的内切圆,∠ACB=90°,若∠BOC=105°,AB=12cm,求BC的长.
如图,⊙O为Rt△ABC的内切圆,∠ACB=90°,若∠BOC=105°,AB=12cm,求BC的长.