题目内容
阅读下面材料:
小明遇到下面一个问题:
如图1所示, 是
是 的角平分线,
的角平分线,  ,求
,求 的值.
的值.
小明发现,分别过 ,
, 作直线
作直线 的垂线,垂足分别为
的垂线,垂足分别为 .通过推理计算,可以解决问题(如图2).请回答,
.通过推理计算,可以解决问题(如图2).请回答, ________.
________.

参考小明思考问题的方法,解决问题:
如图3,四边形 中,
中, 平分
平分 ,
, ,
, .
. 与
与 相交于点
相交于点 .
.

(1) =______.
=______.
(2) =__________.
=__________.
 ;(1)
;(1) (2)
(2) .
.
【解析】
试题分析:应用相似三角形的判定,证得△ABE∽△ACF,根据相似三角形的性质得 ,再证明△BDE∽△CDF,得到
,再证明△BDE∽△CDF,得到 ,进而得到
,进而得到 .
.
(1)借助小明得到的结论,易得 ,得到比值.
,得到比值.
(2) .
.
试题解析: 由作法可知:∠BAD=∠CAD,∠AEB=∠AFC=90°,
∴△ABE∽△ACF,
∴ ,
,
∵∠BDE=∠CDF,∠AEB=∠AFC=90°,
∴△BDE∽△CDF,
∴ ,
,
∴ .
.
(1)借助上面的结论可知: ;
;
(2)∵ ,∴
,∴ .
.
故答案为: ;(1)
;(1) (2)
(2) .
.
考点:1、相似三角形的判定和性质;2、特殊角的三角函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -12x+35=0的根,则该三角形的周长为( )
-12x+35=0的根,则该三角形的周长为( ) 是⊙
是⊙ 的弦,
的弦, 是⊙
是⊙ ,垂足为
,垂足为 .
. ,求
,求 长.
长.
 的图象分布在第二、四象限,则
的图象分布在第二、四象限,则 的取值范围是______.
的取值范围是______.
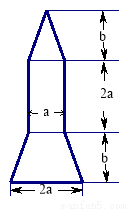
 的式子表示该截面的面积
的式子表示该截面的面积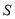 ;
;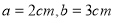 时,求这个火箭模型截面的面积.
时,求这个火箭模型截面的面积.