题目内容
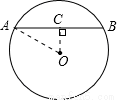
如图, 是⊙
是⊙ 的弦,
的弦, 是⊙
是⊙ 的直径,
的直径, ,垂足为
,垂足为 .
. ,求
,求 长.
长.

 .
.
【解析】
试题分析:连接OB,应用勾股定理求出BE的长,然后应用垂径定理得到AB=2BE,从而求出AB的长.
试题解析:【解析】
∵CE=1,DE=3,
∴CD=CE+DE=4,
∴r=2;
∴OE=DE-OB=1,
连结OB.
在 中,
中, ,
,
∵CD是⊙ 的直径,
的直径, 是⊙
是⊙ 的弦,
的弦,
 ,垂足为
,垂足为 ,
,
∴AB=2BE= .
.

考点:1、勾股定理;2、垂径定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (B)
(B) (C)
(C) (D)
(D)
 是
是 的角平分线,
的角平分线,  ,求
,求 的值.
的值. ,
, 作直线
作直线 .通过推理计算,可以解决问题(如图2).请回答,
.通过推理计算,可以解决问题(如图2).请回答, ________.
________.
 中,
中, 平分
平分 ,
, ,
, .
. 与
与 相交于点
相交于点 .
.
 =______.
=______. =__________.
=__________. 放置在平面直角坐标系中,顶点
放置在平面直角坐标系中,顶点 与坐标原点
与坐标原点 重合,点
重合,点 在
在 轴上.将正方形
轴上.将正方形 第一次落在
第一次落在 点的坐标是________,
点的坐标是________,
 ,
, ,
, ,
, ,则
,则 的值等于( ).
的值等于( ).
 B.
B.  C.
C. D.
D. 
 |÷|
|÷| -
- | -
| - ×
× .
. ,其中
,其中 ,y=-2.
,y=-2.