题目内容
5. 如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2=4.
如图,直线l⊥x轴于点P,且与反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为2,则k1-k2=4.
分析 由反比例函数的图象过第一象限可得出k1>0,k2>0,再由反比例函数系数k的几何意义即可得出S△OAP=$\frac{1}{2}$k1,S△OBP=$\frac{1}{2}$k2,根据△OAB的面积为2结合三角形之间的关系即可得出结论.
解答 解:∵反比例函数y1=$\frac{{k}_{1}}{x}$(x>0)及y2=$\frac{{k}_{2}}{x}$(x>0)的图象均在第一象限内,
∴k1>0,k2>0.
∵AP⊥x轴,
∴S△OAP=$\frac{1}{2}$k1,S△OBP=$\frac{1}{2}$k2.
∴S△OAB=S△OAP-S△OBP=$\frac{1}{2}$(k1-k2)=2,
解得:k1-k2=4.
故答案为:4.
点评 本题考查了反比例函数与一次函数的交点问题已经反比例函数系数k的几何意义,解题的关键是得出S△OAB=$\frac{1}{2}$(k1-k2).本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k的几何意义用系数k来表示出三角形的面积是关键.

练习册系列答案
相关题目
20.下列运算正确的是( )
| A. | a2+a2=a4 | B. | (-b2)3=-b6 | C. | 2x•2x2=2x3 | D. | (m-n)2=m2-n2 |
10.下列运算结果正确的是( )
| A. | a+2b=3ab | B. | 3a2-2a2=1 | C. | a2•a4=a8 | D. | (-a2b)3÷(a3b)2=-b |
17.下列命题中,错误的是( )
| A. | 两组对边分别平行的四边形是平行四边形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 有一组邻边相等的平行四边形是菱形 | |
| D. | 内错角相等 |
14.为缓解中低收入人群和新参加工作的大学生住房的需求,某市将新建保障住房3600000套,把3600000用科学记数法表示应是( )
| A. | 0.36×107 | B. | 3.6×106 | C. | 3.6×107 | D. | 36×105 |
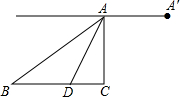 如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30$\sqrt{3}$m到达A′处,
如图,某无人机于空中A处探测到目标B,D,从无人机A上看目标B,D的俯角分别为30°,60°,此时无人机的飞行高度AC为60m,随后无人机从A处继续飞行30$\sqrt{3}$m到达A′处,
