题目内容
5.已知关于x的方程x2-mx+m-3=0,(1)若该方程的一个根为-1,求m的值及该方程的另一根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
分析 (1)把x=-1代入方程x2-mx+m-3=0,得到一个关于m的一元一次方程,求出方程的解和m的值即可;
(2)求出△的值,再比较出其大小即可.
解答 解:(1)∵关于x的方程x2-mx+m-3=0的一个根是-1,
∴x=-1满足关于x的方程x2-mx+m-3=0,
∴1+m+m-3=0,
解得m=1.
设方程的另一根为t,则(-1)t=-2,
∴t=2,
∴方程的另一根为-2;
(2)∵△=(-m)2-4(m-3)=(m-2)2+8>0,
∴不论m取何实数,该方程都有两个不相等的实数根.
点评 本题考查了一元二次方程根的定义和判别式,根与系数的关系,熟知一元二次方程的根与△的关系是解答此题的关键.

练习册系列答案
相关题目
10.下列等式不一定成立的是( )
| A. | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$(b≠0) | B. | a3•a-5=$\frac{1}{{a}^{2}}$(a≠0) | C. | a2-4b2=(a+2b)(a-2b) | D. | (-2a3)2=4a6 |
8.股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一只股票某天跌停,之后两天时间又涨回到原价.若这两天此股票股价的平均增长率为x,则x满足的方程是( )
| A. | (1+x)2=$\frac{11}{10}$ | B. | (1+x)2=$\frac{10}{9}$ | C. | 1+2x=$\frac{11}{10}$ | D. | 1+2x=$\frac{10}{9}$ |
10.下列命题正确的是( )
| A. | 三条直线两两相交有三个交点 | |
| B. | 在平面内,过一点有且只有一条直线与已知直线平行 | |
| C. | 同旁内角互补 | |
| D. | 直线外一点与直线上所有点的连线段中,垂线段最短 |
17.做重复试验:抛掷同一枚啤酒瓶盖1000次.经过统计得“凸面向上”的次数约为420次,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
| A. | 0.22 | B. | 0.42 | C. | 0.50 | D. | 0.58 |
15.若$\frac{3xy}{2x+3y}$中的x和y都扩大到原来的2倍,那么分式的值( )
| A. | 缩小为原来的一半 | B. | 不变 | ||
| C. | 扩大到原来的2倍 | D. | 扩大到原来的4倍 |
 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了1000米.
如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了1000米.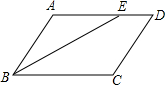 如图,平行四边形ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,平行四边形ABCD的周长20.
如图,平行四边形ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,平行四边形ABCD的周长20.