题目内容
(1)如图1,?ABCD,AE⊥BD,CF⊥BD,则AE、CF满足的数量关系是 ;
(2)如图2,P为AD边上一点,过A、C、D三点分别作BP的垂线,垂足分别为E、F、G,判断线段AE、CF、DG之间的数量关系并证明;

(3)如图3,P为AD延长线上任一点,过A、C、D三点分别作BP的垂线,垂足分别为E、F、G,则线段AE、CF、DG之间的数量关系是 .(不需要证明)
(2)如图2,P为AD边上一点,过A、C、D三点分别作BP的垂线,垂足分别为E、F、G,判断线段AE、CF、DG之间的数量关系并证明;

(3)如图3,P为AD延长线上任一点,过A、C、D三点分别作BP的垂线,垂足分别为E、F、G,则线段AE、CF、DG之间的数量关系是
考点:相似三角形的判定与性质,全等三角形的判定与性质,平行四边形的性质
专题:开放型
分析:(1)根据平行四边形的性质得到AB=CD,AB∥CD,则∠ABE=∠FDC,易证得Rt△ABE≌Rt△CDF,即可得到AE=CF;
(2)过D点作DH⊥CF于H点,如图②,由CF⊥BP,DG⊥BP得到四边形DHFG为矩形,则DG=FH,由GF∥DH得∠APB=∠ADH,再由AD∥BC得到∠APB=∠PBC,则∠ADH=∠PBC,
根据平行四边形的性质得到∠ABC=∠ADC,得到∠ABE=∠CDH,易证Rt△ABE≌Rt△CDH,则AE=CH,因此CF=CH+FH=AE+DG;
(3)过D点作DH⊥AE于H点,如图③,易得四边形DGEH为矩形,则DG=EH,与(2)类似证RtADH≌Rt△CBF得到AH=CF,则有结论AE-DG=CF.
(2)过D点作DH⊥CF于H点,如图②,由CF⊥BP,DG⊥BP得到四边形DHFG为矩形,则DG=FH,由GF∥DH得∠APB=∠ADH,再由AD∥BC得到∠APB=∠PBC,则∠ADH=∠PBC,
根据平行四边形的性质得到∠ABC=∠ADC,得到∠ABE=∠CDH,易证Rt△ABE≌Rt△CDH,则AE=CH,因此CF=CH+FH=AE+DG;
(3)过D点作DH⊥AE于H点,如图③,易得四边形DGEH为矩形,则DG=EH,与(2)类似证RtADH≌Rt△CBF得到AH=CF,则有结论AE-DG=CF.
解答:解:(1)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠FDC,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠DFC=90°,
∴Rt△ABE≌Rt△CDF,
∴AE=CF;
故答案为AE=CF;
(2)线段AE、CF、DG之间的数量关系为:AE+DG=CF.理由如下:
过D点作DH⊥CF于H点,如图②,
∵CF⊥BP,DG⊥BP,
∴四边形DHFG为矩形,
∴DG=FH,∠APB=∠ADH,
又∵AD∥BC,
∴∠APB=∠PBC,
∴∠ADH=∠PBC,
∵四边形ABCD为平行四边形,
∴∠ABC=∠ADC,
∴∠ABE=∠CDH,
而∠AEB=90°,
在△ABE和△CDH中,
AB=CD
∠ABE=∠CDH
∠AEB=∠DHC=90°
∴Rt△ABE≌Rt△CDH,
∴AE=CH,
∴CF=CH+FH=AE+DG;
(3)过D点作DH⊥AE于H点,如图③,
∵AE⊥BP,DG⊥BP,
∴四边形DGEH为矩形,
∴DG=EH,
∵DH∥BP,
∴∠ADH=∠P
而AP∥BC,
∴∠P=∠PBC,
∴∠ADH=∠CBF,
而AD=BC,CF⊥BF,
∴Rt△ADH≌Rt△CBF,
∴AH=CF,
∴AE-AH=HE,
∴AE-CF=DG,
即AE-DG=CF.
∴AB=CD,AB∥CD,
∴∠ABE=∠FDC,
又∵AE⊥BD,CF⊥BD,
∴∠AEB=∠DFC=90°,
∴Rt△ABE≌Rt△CDF,
∴AE=CF;
故答案为AE=CF;
(2)线段AE、CF、DG之间的数量关系为:AE+DG=CF.理由如下:

过D点作DH⊥CF于H点,如图②,
∵CF⊥BP,DG⊥BP,
∴四边形DHFG为矩形,
∴DG=FH,∠APB=∠ADH,
又∵AD∥BC,
∴∠APB=∠PBC,
∴∠ADH=∠PBC,
∵四边形ABCD为平行四边形,
∴∠ABC=∠ADC,
∴∠ABE=∠CDH,
而∠AEB=90°,
在△ABE和△CDH中,
AB=CD
∠ABE=∠CDH
∠AEB=∠DHC=90°
∴Rt△ABE≌Rt△CDH,
∴AE=CH,
∴CF=CH+FH=AE+DG;
(3)过D点作DH⊥AE于H点,如图③,
∵AE⊥BP,DG⊥BP,
∴四边形DGEH为矩形,
∴DG=EH,
∵DH∥BP,
∴∠ADH=∠P
而AP∥BC,
∴∠P=∠PBC,
∴∠ADH=∠CBF,
而AD=BC,CF⊥BF,
∴Rt△ADH≌Rt△CBF,
∴AH=CF,
∴AE-AH=HE,
∴AE-CF=DG,
即AE-DG=CF.
点评:本题考查了全等三角形的判定与性质:有一条边对应相等,并且有两组角对应相等的两个三角形全等;全等三角形的对应边相等.也考查了平行四边形的性质.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 某班的元旦晚会上,有一个转盘摇奖游戏.如图有甲、乙两个转盘,参与者只能选择其中的一个.当转盘停止时,指针落在哪一区域就可获得相应的奖品.如果小颖想得到“铅笔”,她应选择( )
某班的元旦晚会上,有一个转盘摇奖游戏.如图有甲、乙两个转盘,参与者只能选择其中的一个.当转盘停止时,指针落在哪一区域就可获得相应的奖品.如果小颖想得到“铅笔”,她应选择( )| A、乙转盘 |
| B、甲转盘 |
| C、甲、乙转盘均可 |
| D、无法选择哪个转盘 |
 如图,15个外径为1m的钢管以如图方式堆放,为了防雨,需要搭建防雨棚的高度最低应为( )m.
如图,15个外径为1m的钢管以如图方式堆放,为了防雨,需要搭建防雨棚的高度最低应为( )m.A、2
| ||||
B、
| ||||
| C、5 | ||||
D、2
|
一次函数y=
x-15的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有( )
| 5 |
| 4 |
| A、90个 | B、92个 |
| C、104个 | D、106个 |

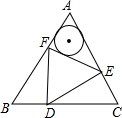 已知:如图,边长为a的正△ABC内有一边长为b的正△DEF,且a-b=2,则△AEF的内切圆半径为
已知:如图,边长为a的正△ABC内有一边长为b的正△DEF,且a-b=2,则△AEF的内切圆半径为 As in the figure,there are four circle with radius of 2.The four circles are apart from each other.Link their centers to form a quadrilateral,then the total area of the shaded parts in the figure is( )
As in the figure,there are four circle with radius of 2.The four circles are apart from each other.Link their centers to form a quadrilateral,then the total area of the shaded parts in the figure is( )